Контрольная работа: Математические модели физико-химических процессов

lgμ_см =х₁ lgμ₁ +х₂ lgμ₂ +…+х_n lgμ_n ,

где μ₁ , μ₂ – динамические коэффициенты вязкости отдельных компонентов; х₁ , х₂ – мольные доли компонентов в смеси.

Молекулярно-кинетическая теория объясняет вязкость движением и взаимодействием молекул. В газах расстояния между молекулами существенно больше радиуса действия молекулярных сил, поэтому вязкость газов определяется главным образом молекулярным движением. Между движущимися относительно друг друга слоями газа происходит постоянный обмен молекулами, обусловленный их непрерывным хаотическим (тепловым) движением. Переход молекул из одного слоя в соседний, движущийся с иной скоростью, приводит к переносу от слоя к слою определённого количества движения. В результате медленные слои ускоряются, а более быстрые замедляются. Работа внешней силы F, уравновешивающей вязкое сопротивление и поддерживающей установившееся течение, полностью переходит в теплоту.

Вязкость идеального газа не зависит от его плотности (давления), так как при сжатии газа общее количество молекул, переходящих из слоя в слой, увеличивается, но зато каждая молекула менее глубоко проникает в соседний слой и переносит меньшее количество движения (закон Максвелла). Для вязкости идеальных газов в молекулярно-кинетической теории даётся следующее соотношение:

,

Где ρ – число молекул в единице объема; (ν) – средняя скорость теплового движения молекул, λ – средняя длина свободного пробега

Изменение динамического коэффициента вязкости газов с температурой выражается формулой:

,

где μ₀ – динамический коэффициент вязкости при 0єС; Т – температура, К; С – постоянная Сатерленда

Зависимость вязкости жидкостей от давления выражается уравнением :

,

где μ_р и μ₀ - динамическая вязкость при давлении p и атмосферном давлении, Па∙с; e - основание натуральных логарифмов; α_р - пьезокоэффициент вязкости, Па^-1 ∙с^-1 (для нефтяных масел лежит в пределах 0,001-0,004).

При высоком давлении вязкость может возрасти настолько, что масло потеряет свойства жидкости и превратится в квазипластичное тело. При давлении более 1015 Па минеральное масло превращается в твердое тело. При снятии нагрузки первоначальная вязкость восстанавливается. Вязкость масел при всех температурах с увеличением давления растет неодинаково и тем значительнее, чем выше давление и ниже температура

Динамическая вязкость воды при 4єС принята равной 1,005·10^–3 Н·c/м² = 1,005 мН·с/м² ~ 1 спз. Кинематическая вязкость воды при 4єС принята равной 1,0068·10^–6 м² /с.

Динамический коэффициент вязкости воздуха при температуре 0єС и атмосферном давлении μ=17.20∙10^-6 Па∙с.

3. Напишите основное уравнение гидростатики. Из какого уравнения его получают, примеры практического применения. Как рассчитывается давление жидкости на дно и стенки сосуда?

Основное уравнение гидростатики:

,

где z₁ , z₂ – высота погружения двух точек жидкости; р₀ , р – гидростатическое давление в этих точках соответственно; γ – удельный вес жидкости. Часто основное уравнение гидростатики записывают в следующем виде:

р=р₀ +ρgh,

где р – гидростатическое давление на глубине h от поверхности жидкости; р₀ – давление жидкости на поверхности жидкости; ρ – плотность жидкости; g – ускорение свободного падения.

Выводится основное уравнение гидростатики из системы дифференциальных уравнений Эйлера:

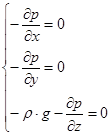
Из основного уравнения гидростатики следует равенство уровней в сообщающихся сосудах, а также закон Архимеда, закон Паскаля.

Если жидкость поместить в какой-либо сосуд, то гидростатическое давление на отдельные части площади горизонтального дна сосуда везде одинаково, давление же на боковые стенки возрастает с увеличением глубины погружения; при этом давление на дно сосуда не зависит от формы или угла наклона боковых стенок:

Р = р₀ +ρgН

Общее давление Р на горизонтальное дно не зависит от формы сосуда и объема жидкости в нем:

Р = рF,

Где F – площадь дна сосуда.