Контрольная работа: Математическое моделирование в управлении
0,4
Рис. 6. Линии тренда.
Алгоритм содержит такие действия:
- разместить на рабочем листе Excel в двух смежных столбцах исходные данные таким образом, чтобы первым был независимый показатель;
- Вставка – Диаграмма – Точечная (первый вариант) – Далее;
- на закладке Диапазон данных ввести диапазон , занимаемый всей таблицей, для чего выделить мышью оба столбца ;
- на закладке Ряд ввести в поле Значения X диапазон значений независимой величины , а в поле Значения Y диапазон значений величины, регрессию которой следует оценить (см.рис.7 );
Далее – на закладке Заголовки ввести заголовки осей и диаграммы – Далее – указать, где разместить диаграмму (на имеющемся листе) – Готово;
- откорректировать появившуюся диаграмму, особенно формат осей и надписи, для чего щелкнуть правой кнопкой мыши по оси или надписи и в появившемся маленьком диалоговом окне щелкнуть по пункту Формат оси (или надписи) ;
- появившемся диалоговом окне Формат оси (или надписи ) выбрать нужную закладку и внести необходимые изменения – OK ;
- откорректировать полученное корреляционное поле, исключив резко выделяющиеся из общего множества отдельные точки;
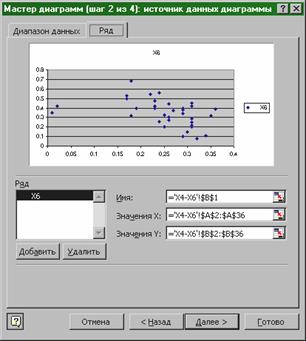
Рис.7. Построение корреляционного поля.
- щелкнуть правой кнопкой мыши по любой точке диаграммы и в появившемся диалоговом окне выбрать пункт меню Добавить линию тренда;
- в появившемся диалоговом окне на закладке Тип выбрать тип зависимости: линейный или полиномиальный (указать порядок приближения);
- щелкнуть по закладке Параметры и в появившемся после этого диалоговом окне щелкнуть пункты показывать уравнение на диаграмме и поместить на диаграмму величину достоверности аппроксимации ( R ^2);
- записать уравнение регрессии, заменив y и x на имена результативного и факторного признаков соответственно и оценить значимость полученного уравнения с помощью R^2.
На рис.6 приведены: точечная диаграмма зависимости X6 от X4 и две линии тренда – линейная и нелинейная. Уравнение первой совпадает с уравнением линией регрессии, полученным с помощью инструмента Регрессия . Вторая имеет уравнение , т.е. оценку линии регрессии, такого вида:
![]() .
.
Причем коэффициент детерминации в первом случае равен 0,3688 , а для кубической зависимости R2 = 0,4762 , т.е. предпочтительнее использовать полиномиальную зависимость как лучше согласующуюся со статистическими данными.
Для остальных двух отобранных пар факторных признаков необходимо выполнить такие же действия и получить аналогичные оценки функций регрессии.
§1.5 Регрессионный анализ трехмерной модели
Для исследования статистической зависимости одного результирующего признака от двух и более факторных признаков в Excel есть две возможности: инструмент Регрессия для случая линейной статистической зависимости и непосредственное применение метода наименьших квадратов в случае зависимости любого вида.
Алгоритм применения инструмента Регрессия отличается от описанного выше для случая двумерной модели только количеством исходных данных, размещаемых на рабочем листе и соответственно диапазоном входных параметров , вводимом в диалоговом окне Регрессия . Выходные данные также отличаются только количеством информации при сохранении их смысла.
|
Регрессионная статистика | |
|
Множественный R |
0,762322 |
|
R-квадрат |
0,581135 |
|
Нормированный R-квадрат |
К-во Просмотров: 565
Бесплатно скачать Контрольная работа: Математическое моделирование в управлении
|