Контрольная работа: Математичне моделювання економічних систем
Отриманий план не оптимальний
Обраний ключовий елемент (2,5)
| I | базис | Cб | P0 | 2 | 3 | 0 | 0 | 0 | -M |
| P1 | P2 | P3 | P4 | P5 | P6 | ||||
| 1 | P3 | 0 | 6 | 5 | 0 | 1 | -2 | 0 | 0 |
| 2 | P5 | 0 | 2 | -2 | 0 | 0 | 1 | 1 | -1 |
| 3 | P2 | 3 | 6 | -1 | 1 | 0 | 1 | 0 | 0 |
| 4 | 18 | -5 | 0 | 0 | 3 | 0 | 0 | ||
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | -1 |
Отриманий план не оптимальний
Обраний ключовий елемент (1,1)
| I | базис | Cб | P0 | 2 | 3 | 0 | 0 | 0 | -M |
| P1 | P2 | P3 | P4 | P5 | P6 | ||||
| 1 | P1 | 2 | 6/5 | 1 | 0 | 1/5 | -2/5 | 0 | 0 |
| 2 | P5 | 0 | 22/5 | 0 | 0 | 2/5 | 1/5 | 1 | -1 |
| 3 | P2 | 3 | 36/5 | 0 | 1 | 1/5 | 3/5 | 0 | 0 |
| 4 | 24 | 0 | 0 | 1 | 1 | 0 | 0 | ||
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
План оптимальний
Розв’язок : X* (
,
) F* =24;
Розв’язок двоїстої задач
Побудуємо двоїсту функцію
3. 
,
Система обмежень
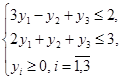
Скористаємось теоремою
Якщо задача лінійного програмування в канонічній формі (7)-(9) має оптимальний план 
, то 
є оптимальним планом двоїстої задачі
,
,
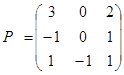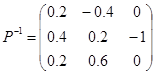
Розв’язок:
Fmin * = 9,6;
Завдання 2. Задача цілочислового програмування
Для задачі із завдання 1, як для задачі цілочислового програмування, знайти розв’язки геометричним методом і методом Гоморі.
Розв ′язання геометричним методом
,
 |
|
|
|
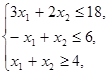
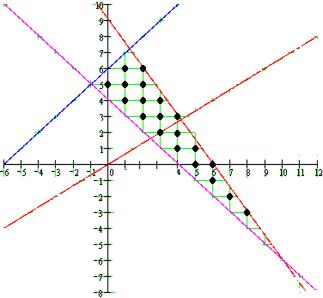
Відповідь: 
Розв ′язання методом Гомор і
Наведемо останню симплекс-таблицю
| I | базис | Cб | P0 | 2 | 3 | 0 | 0 | 0 | -M |
| P1 | P2 | P3 | P4 | P5 | P6 | ||||
| 1 | P1 | 2 | 6/5 | 1 | 0 | 1/5 | -2/5 | 0 | 0 |
| 2 | P5 | 0 | 22/5 | 0 | 0 | 2/5 | 1/5 | 1 | -1 |
| 3 | P2 | 3 | 36/5 | 0 | 1 | 1/5 | 3/5 | 0 | 0 |
| 4 | 24 | 0 | 0 | 1 | 1 | 0 | 0 | ||
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Побудуємо нерівність Гоморі за першим аргументом.
