Контрольная работа: Математичне моделювання економічних систем
![]()
![]()
![]()
![]()
![]()
![]()
| I | базис | Cб | P0 | 2 | 3 | 0 | 0 | 0 | 0 |
| P1 | P2 | P3 | P4 | P5 | P7 | ||||
| 1 | P1 | 2 | 6/5 | 1 | 0 | 1/5 | -2/5 | 0 | 0 |
| 2 | P5 | 0 | 22/5 | 0 | 0 | 2/5 | 1/5 | 1 | 0 |
| 3 | P2 | 3 | 36/5 | 0 | 1 | 1/5 | 3/5 | 0 | 0 |
| 4 | P7 | 0 | -1/5 | 0 | 0 | -1/5 | -3/5 | 0 | 1 |
| 5 | 24 | 0 | 0 | 1 | 1 | 0 | 0 |
Обраний розв’язковий елемент (4,4)
| I | базис | Cб | P0 | 2 | 3 | 0 | 0 | 0 | 0 |
| P1 | P2 | P3 | P4 | P5 | P7 | ||||
| 1 | P1 | 2 | 1 | 1 | 0 | 0 | -1 | 0 | 0 |
| 2 | P5 | 0 | 4 | 0 | 0 | 0 | 11/5 | 1 | 0 |
| 3 | P2 | 3 | 7 | 0 | 1 | 0 | 0 | 0 | 0 |
| 4 | P4 | 0 | 2 | 0 | 0 | 1 | 3 | 0 | 1 |
| 5 | 14 | 0 | 0 | 0 | 2 | 0 | 0 |
Отриманий план являється оптимальним і цілочисельним.
Розв’язок : X* (1,7) Fmax * =23;
Відповідь: цілочисельною точкою максимуму даної задачі є точка (1,7)
Завдання 3. Задача дробово-лінійного програмування
Для задачі дробово-лінійного програмування знайти розв’язки геометричним методом і симплекс-методом:
![]() ,
,
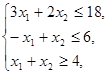
![]()
Розв ′язання геометричним методом
![]()
![]()
![]()
![]()
![]()
Визначимо, в яку сторону потрібно обертати пряму навколо початку координат, щоб значення цільової функції збільшувалось. Таким чином ми визначимо яка з крайніх точок є точкою максимуму.
f (1;0) = 2/3 f (0;1) = 3/7
Тобто при крутінні прямої проти годинникової стрілки значення цільової функції зменшується.
Використаємо результати обчислень і геометричних побудов з попереднього завдання.
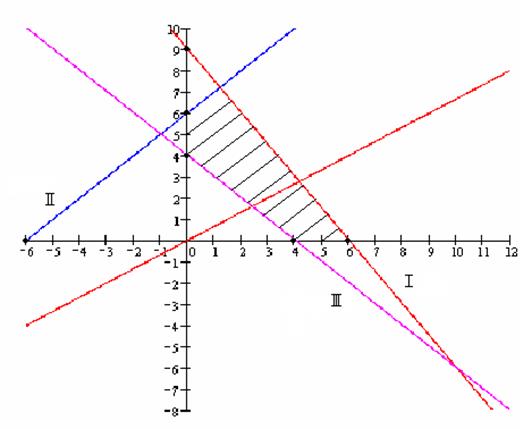
З графіка очевидно, що розв’язок лежить на перетині двох прямих. Для визначення точки перетину прямої І та ІІ розв′яжемо систему з двох рівнянь.

![]()