Контрольная работа: Методы решения систем линейных уравнений

для решения этой линейной системы уравнений, конечно, можно применять метод Гаусса, но тогда пришлось бы делать много необязательных операций с нулями. Чтобы сэкономить время вычислений и не работать лишний раз с нулями, Томас (1949г.) разработал специальный алгоритм расчета. Рассчитывая по алгоритму Томаса элементы получаемой треугольной матрицы, мы следуем методу Гаусса, с уточнением, что с нулями никаких действий не производим; алгоритм Томаса называют – методом прогонки.

Для решения системы (40) методом прогонки – Томаса действуем следующим образом:

а) прямой ход:

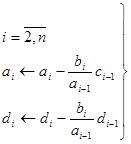(41)

Замечание: после проведения прямого хода предполагается, что все , и - неизменны (что очевидно).

б) обратный ход:

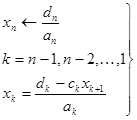(42)

Таким образом, для системы линейных уравнений с трехдиаганальной матрицей наиболее экономным является алгоритм прогонки – Томаса, который является «отфильтрованным» методом Гаусса.

Метод минимизации невязки для решения линейной системы уравнений (метод наименьших квадратов).

При проведении экспериментов, часто приходится решать следующую задачу: определить известных ,которые непосредственно не измеряются, а измеряются величины связанные с определяемыми переменными . Измерения не свободны от случайных ошибок, которыми нельзя пренебречь.

Число наблюдаемых величин больше числа неизвестных . Пусть известно, что величины связаны между собой линейной зависимостью:

, , . (43)

Коэффициенты - считаются известными и неотягощенными случайными ошибками. Система (43) называется системой условных уравнений.

Если бы все числа были точными, то неизвестные , могли бы быть определены из любых - уравнений системы . Но так, как - определены с ошибками, то система условных уравнений несовместна (переопределена, т.к. ), существуют «невязки»:

, (44)

задача теперь заключается в том, чтобы найти такие значения , при которых функция невязки - минимально по некоторой норме, т.е. мы ищем такие , при которых норма невязки - минимальна.

В методе наименьших квадратов, в качестве нормы рассматривают дискретную норму Гаусса:

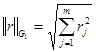(45)

Очевидно, что эта норма минимальна тогда, когда минимально подкоренное выражение, т.е. сумма квадратов невязок .

(46)

Условия существования минимума для функций специального вида имеют вид:

,, (47)

т.е. задача сводится, как и в общей теории приближений, к решению системы нормальных уравнений.

Для примера рассмотрим уравнений с тремя неизвестными, система условных уравнений имеет вид:

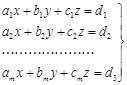(48)

Тогда система соответствующих нормальных уравнений имеет вид:

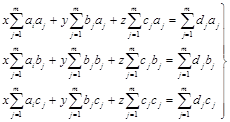(49)

Решение системы (49) дает решение задачи (48) наилучшим приближением, в смысле дискретной нормы Гаусса.

Замечания: