Контрольная работа: Многомерные и многосвязные системы

,

.

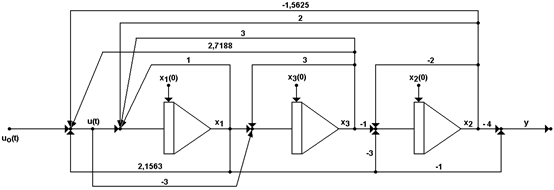
Рис. 8. Структура синтезированной системы

2. Построение наблюдателя полного порядка

Система

называется асимптотическим наблюдателем полного порядка, если для любого начального состояния х(0) и всех оценка с ростом времени асимптотически приближается к вектору состояния .

Найдём структуру асимптотического наблюдателя, для чего определим ошибку восстановления и найдём модель её изменения:

.

Затем потребуем, чтобы при всех и .

Это равенство возможно при:

,

.

Таким образом, структура асимптотического наблюдателя полного порядка определяется моделью вида:

.

На рис. 9 изображена структура системы и её наблюдателя.

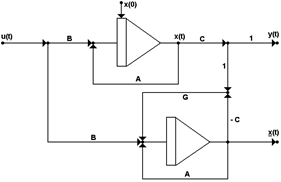
Рис. 9. Структура системы с наблюдателем

Задача синтеза наблюдателя системы состоит в том, чтобы найти матрицу . Это можно сделать, исходя из условия асимптотической сходимости оценки к вектору состояния при любых начальных состояниях наблюдателя и системы.

Пусть ошибка восстановления , тогда

.

Ошибка восстановления описывается линейным однородным дифференциальным уравнением с матрицей и ненулевыми начальными условиями, а поэтому асимптотическая сходимость ошибки к нулю возможна тогда и только тогда, когда собственные числа матрицы , которые называют полюсами наблюдателя, располагаются в левой полуплоскости.

Пусть матрица

,

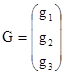тогда матрица

.

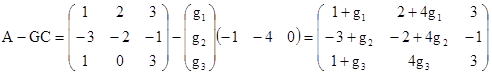Полюса наблюдателя определяются уравнением:

.
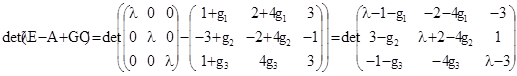