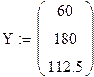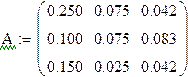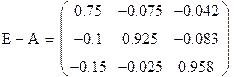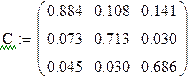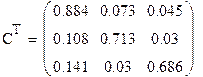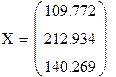Контрольная работа: Моделирование макроэкономических процессов и систем

240

Решить задачу межотраслевого баланса, если конечное потребление первой отрасли не изменилось, второй отрасли увеличилось в 1,5 раза, третьей уменьшилось на 25%.

С учетом изменений строим новый вектор конечного потребления:

Находим матрицу прямых затрат в условиях взаимодействия трех отраслей:

Т.к. a_ij ≥ 0, = 0.5 ≤ 1, = 0.175 ≤ 1, = 0.167 ≤ 1 –

матрица A продуктивна, следовательно, продуктивна и сама модель.

Находим матрицу E-A, представляющую собой матрицу полных затрат, каждый элемент которой выражает стоимостные затраты той части валового выпуска которая необходима для выпуска единицы конечного продукта.

Определитель матрицы:

Вычислим матрицу C составленную из алгебраических дополнений матрицы E-A:

И транспонируем ее:

Находим новый вектор валового выпуска продукции тремя отраслями:

Чтобы машиностроение дало 60 у.д.е., металлургия 120 у.д.е., энергетика 150 у.д.е. конечного продукта идущего на непроизводственное потребление необходимо обеспечить следующие объемы валового выпуска отраслей: Машиностроение - 109,772 у.д.е.

Металлургия – 212,934 у.д.е.

Энергетика – 140,269 у.д.е.

Задание 5. Динамическая экономико-математическая модель Кейнса

Экономика в форме динамической модели Кейнса как инерционное звено

В этой модели предполагается, что ВВП в следующем году равен совокупному спросу предыдущего (текущего) года, а совокупный спрос, состоящий из спроса на потребительские (C) и инвестиционные (I) товары, зависит только от ВВП текущего года: