Контрольная работа: Моделирование макроэкономических процессов и систем
![]()
Если приращение инвестиций ΔI сравнительно мало, то при эволюторном характере функции f(y,I) переменная часть η(t) также сравнительно мала. Поэтому правую часть можно разложить в окрестности точки (y0 ,I0 ) в ряд Тейлора, отбросив члены второго и более высоких порядков:
![]()
После перенесения члена, содержащего η, в левую часть и деления обеих частей на
![]()
получаем уравнение инерционного звена:
![]()
где
![]()
– обобщенная предельная склонность к сбережению в начальном состоянии;
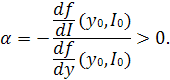
Из вышеописанного вытекает, что переменная часть ВВП будет вести себя следующим образом:
![]()
а ВВП в целом будет изменяться как функция
![]()
При этом новое равновесное состояние ВВП

Заключение
В данной курсовой работе были рассмотрены основные математические модели макроэкономических процессов, такие как мультипликативная производственная функция, кривая Лоренца, различные модели банковских операций, модели межотраслевого баланса Леонтьева, динамическая экономико-математическая модель Кейнса.
Как можно было заключить из вышеизложенного, математические методы имеют большую степень универсальности. Основой этой универсальности является язык математики. Если исследователи различных специальностей часто говорят об одной и той же проблеме совершенно по-разному, видят разные ее особенности, и не могут связать их воедино; то перевод проблемы на математический язык сразу выявляет общие закономерности, и даже может дать уже практически готовое решение, полученное ранее где-то в другой отрасли знаний и для других целей. То есть предпосылкой использования математики является формализация количественных и качественных сторон проблемы.
Литература
1. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем. М.: Финансы и статистика, 2005. 368 с.
2. Ильченко А.Н. Экономико-математические методы. М.: Финансы и статистика, 2006 287 с.
3. Колемаев В.А. Экономико-математическое моделирование: Моделирование макроэкономических процессов и систем. М.: ЮНИТИ, 2005 295 с.
4. Колемаев В.А. Математическая экономика. М.: ЮНИТИ, 2005. 399 с.
5. Найденков В.И. Прогнозирование и моделирование национальной экономики: Конспект лекций. М.: ПРИОР, 2004. 156 с.
6. Орехов Н.А., Левин А.Г., Горбунов Е.А., Математические методы и модели в экономике. М.: ЮНИТИ, 2004. 302 с.
7. Просветов Г.И. Математические модели в экономике. Спб.: РДЛ, 2006. 151 с.
8. Федосеев В.В. Экономико-математические методы и прикладные модели. М.: ЮНИТИ, 2005 391 с.