Контрольная работа: Моделювання станів транзистора 2Т909Б
xkl – значення k-го фактора в l-му досліді.
X = ![]()
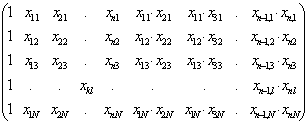 , B =
, B = ![]() , Y =
, Y = ![]() .
.
У матричному вигляді систему записують рівнянням (XT X)B = XT Y. З останнього рівняння очевидно, що коефіцієнти bi визначаються як ![]() , де (XT X)-1 – обернена матриця (XT X). Дисперсію моделювання оцінюють за формулою:
, де (XT X)-1 – обернена матриця (XT X). Дисперсію моделювання оцінюють за формулою:
δмод 2 = 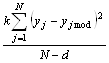 ,
,
де N - кількість дослідів,
d – кількість значущих коефіцієнтів моделі
k – кратність дублювання дослідів
Експериментальні дані та їх обробка
Математичну модель процесу представимо у вигляді полінома, а саме:
Y’ = b0 + b1 Uке + b2 Iб + b3 Uке Iб + b4 Uке 2 + b5 Iб 2 + b6 Uке 2 Iб + b7 Iб 2 Uке +
+ b8 Uке 2 Iб 2,
де Y’ – розрахункове значення струму колектора Ік (мА),
b0 , b1 … – коефіцієнти поліному,
Uке – напруга на колекторно-емітерному переході (В),
Iб – струм бази Іб (мА).
Сімейство ВАХ транзистора 2Т909Б має наступний вигляд (рис.1)
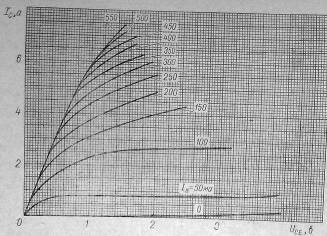
Рис. 1. Вольт-амперні характеристики транзистора 2Т909Б.
Отримані експериментальні данні наведено в табл. 1.
Таблиця 1. Експериментальна залежність ІК (мА) від ІБ та UКЕ для транзистора 2Т909Б
| x0 | x1(Iб) | x2(Uк-э) | x1*x2 | X1^2 | x2^2 | x1*x2^2 | x1^2*x2 | (x1*x2)^2 | Y |
| 1 | 0,05 | 0,2 | 0,01 | 0,0025 | 0,04 | 0,002 | 0,0005 | 0,0001 | 0,5 |
| 1 | 0,05 | 0,4 | 0,02 | 0,0025 | 0,16 | 0,008 | 0,001 | 0,0004 | 0,7 |
| 1 | 0,05 | 0,6 | 0,03 | 0,0025 | 0,36 | 0,018 | 0,0015 | 0,0009 | 0,8 |
| 1 | 0,05 | 0,8 | 0,04 | 0,0025 | 0,64 | 0,032 | 0,002 | 0,0016 | 0,8 |
| 1 | 0,05 | 1 | 0,05 | 0,0025 | 1 | 0,05 | 0,0025 | 0,0025 | 0,8 |
| 1 | 0,05 | 1,2 | 0,06 | 0,0025 | 1,44 | 0,072 | 0,003 | 0,0036 | 0,8 |
| 1 | 0,05 | 1,4 | 0,07 | 0,0025 | 1,96 | 0,098 | 0,0035 | 0,0049 | 0,8 |
| 1 | 0,05 | 1,6 | 0,08 | 0,0025 | 2,56 | 0,128 | 0,004 | 0,0064 | 0,8 |
| 1 | 0,05 | 1,8 | 0,09 | 0,0025 | 3,24 | 0,162 | 0,0045 | 0,0081 | 0,8 |
| 1 | 0,05 | 2 | 0,1 | 0,0025 | 4 | 0,2 | 0,005 | 0,01 | 0,8 |
| 1 | 0,1 | 0,2 | 0,02 | 0,01 | 0,04 | 0,004 | 0,002 | 0,0004 | 1 |
| 1 | 0,1 | 0,4 | 0,04 | 0,01 | 0,16 | 0,016 | 0,004 | 0,0016 | 1,5 |
| 1 | 0,1 | 0,6 | 0,06 | 0,01 | 0,36 | 0,036 | 0,006 | 0,0036 | 1,8 |
| 1 | 0,1 | 0,8 | 0,08 | 0,01 | 0,64 | 0,064 | 0,008 | 0,0064 | 2,1 |
| 1 | 0,1 | 1 | 0,1 | 0,01 | 1 | 0,1 | 0,01 | 0,01 | 2,3 |
| 1 | 0,1 | 1,2 | 0,12 | 0,01 | 1,44 | 0,144 | 0,012 | 0,0144 | 2,5 |
| 1 | 0,1 | 1,4 | 0,14 | 0,01 | 1,96 | 0,196 | 0,014 | 0,0196 | 2,6 |
| 1 | 0,1 | 1,6 | 0,16 | 0,01 | 2,56 | 0,256 | 0,016 | 0,0256 | 2,7 |
| 1 | 0,1 | 1,8 | 0,18 | 0,01 | 3,24 | 0,324 | 0,018 | 0,0324 | 2,7 |
| 1 | 0,1 | 2 | 0,2 | 0,01 | 4 | 0,4 | 0,02 | 0,04 | 2,7 |
| 1 | 0,15 | 0,2 | 0,03 | 0,0225 | 0,04 | 0,006 | 0,0045 | 0,0009 | 1,2 |
| 1 | 0,15 | 0,4 | 0,06 | 0,0225 | 0,16 | 0,024 | 0,009 | 0,0036 | 2 |
| 1 | 0,15 | 0,6 | 0,09 | 0,0225 | 0,36 | 0,054 | 0,0135 | 0,0081 | 2,5 |
| 1 | 0,15 | 0,8 | 0,12 | 0,0225 | 0,64 | 0,096 | 0,018 | 0,0144 | 2,9 |
| 1 | 0,15 | 1 | 0,15 | 0,0225 | 1 | 0,15 | 0,0225 | 0,0225 | 3,1 |
| 1 | 0,15 | 1,2 | 0,18 | 0,0225 | 1,44 | 0,216 | 0,027 | 0,0324 | 3,3 |
| 1 | 0,15 | 1,4 | 0,21 | 0,0225 | 1,96 | 0,294 | 0,0315 | 0,0441 | 3,5 |
| 1 | 0,15 | 1,6 | 0,24 | 0,0225 | 2,56 | 0,384 | 0,036 | 0,0576 | 3,7 |
| 1 | 0,15 | 1,8 | 0,27 | 0,0225 | 3,24 | 0,486 | 0,0405 | 0,0729 | 3,9 |
| 1 | 0,15 | 2 | 0,3 | 0,0225 | 4 | 0,6 | 0,045 | 0,09 | 4 |
| 1 | 0,2 | 0,2 | 0,04 | 0,04 | 0,04 | 0,008 | 0,008 | 0,0016 | 1,2 |
| 1 | 0,2 | 0,4 | 0,08 | 0,04 | 0,16 | 0,032 | 0,016 | 0,0064 | 2,6 |
| 1 | 0,2 | 0,6 | 0,12 | 0,04 | 0,36 | 0,072 | 0,024 | 0,0144 | 3 |
| 1 | 0,2 | 0,8 | 0,16 | 0,04 | 0,64 | 0,128 | 0,032 | 0,0256 | 3,4 |
| 1 | 0,2 | 1 | 0,2 | 0,04 | 1 | 0,2 | 0,04 | 0,04 | 3,8 |
| 1 | 0,2 | 1,2 | 0,24 | 0,04 | 1,44 | 0,288 | 0,048 | 0,0576 | 4 |
| 1 | 0,2 | 1,4 | 0,28 | 0,04 | 1,96 | 0,392 | 0,056 | 0,0784 | 4,3 |
| 1 | 0,2 | 1,6 | 0,32 | 0,04 | 2,56 | 0,512 | 0,064 | 0,1024 | 4,5 |
| 1 | 0,2 | 1,8 | 0,36 | 0,04 | 3,24 | 0,648 | 0,072 | 0,1296 | 4,7 |
| 1 | 0,2 | 2 | 0,4 | 0,04 | 4 | 0,8 | 0,08 | 0,16 | 4,9 |
| 1 | 0,25 | 0,2 | 0,05 | 0,0625 | 0,04 | 0,01 | 0,0125 | 0,0025 | 1,2 |
| 1 | 0,25 | 0,4 | 0,1 | 0,0625 | 0,16 | 0,04 | 0,025 | 0,01 | 2,6 |
| 1 | 0,25 | 0,6 | 0,15 | 0,0625 | 0,36 | 0,09 | 0,0375 | 0,0225 | 3,5 |
| 1 | 0,25 | 0,8 | 0,2 | 0,0625 | 0,64 | 0,16 | 0,05 | 0,04 | 4 |
| 1 | 0,25 | 1 | 0,25 | 0,0625 | 1 | 0,25 | 0,0625 | 0,0625 | 4,4 |
| 1 | 0,25 | 1,2 | 0,3 | 0,0625 | 1,44 | 0,36 | 0,075 | 0,09 | 4,7 |
| 1 | 0,25 | 1,4 | 0,35 | 0,0625 | 1,96 | 0,49 | 0,0875 | 0,1225 | 4,9 |
| 1 | 0,25 | 1,6 | 0,4 | 0,0625 | 2,56 | 0,64 | 0,1 | 0,16 | 5,2 |
| 1 | 0,25 | 1,8 | 0,45 | 0,0625 | 3,24 | 0,81 | 0,1125 | 0,2025 | 5,4 |
| 1 | 0,25 | 2 | 0,5 | 0,0625 | 4 | 1 | 0,125 | 0,25 | 5,5 |
| 1 | 0,3 | 0,2 | 0,06 | 0,09 | 0,04 | 0,012 | 0,018 | 0,0036 | 1,2 |
| 1 | 0,3 | 0,4 | 0,12 | 0,09 | 0,16 | 0,048 | 0,036 | 0,0144 | 2,6 |
| 1 | 0,3 | 0,6 | 0,18 | 0,09 | 0,36 | 0,108 | 0,054 | 0,0324 | 3,8 |
| 1 | 0,3 | 0,8 | 0,24 | 0,09 | 0,64 | 0,192 | 0,072 | 0,0576 | 4,4 |
| 1 | 0,3 | 1 | 0,3 | 0,09 | 1 | 0,3 | 0,09 | 0,09 | 4,8 |
| 1 | 0,3 | 1,2 | 0,36 | 0,09 | 1,44 | 0,432 | 0,108 | 0,1296 | 5,2 |
| 1 | 0,3 | 1,4 | 0,42 | 0,09 | 1,96 | 0,588 | 0,126 | 0,1764 | 5,4 |
| 1 | 0,3 | 1,6 | 0,48 | 0,09 | 2,56 | 0,768 | 0,144 | 0,2304 | 5,7 |
| 1 | 0,3 | 1,8 | 0,54 | 0,09 | 3,24 | 0,972 | 0,162 | 0,2916 | 5,9 |
| 1 | 0,35 | 0,2 | 0,07 | 0,1225 | 0,04 | 0,014 | 0,0245 | 0,0049 | 1,2 |
| 1 | 0,35 | 0,4 | 0,14 | 0,1225 | 0,16 | 0,056 | 0,049 | 0,0196 | 2,6 |
| 1 | 0,35 | 0,6 | 0,21 | 0,1225 | 0,36 | 0,126 | 0,0735 | 0,0441 | 3,8 |
| 1 | 0,35 | 0,8 | 0,28 | 0,1225 | 0,64 | 0,224 | 0,098 | 0,0784 | 4,8 |
| 1 | 0,35 | 1 | 0,35 | 0,1225 | 1 | 0,35 | 0,1225 | 0,1225 | 5,3 |
| 1 | 0,35 | 1,2 | 0,42 | 0,1225 | 1,44 | 0,504 | 0,147 | 0,1764 | 5,6 |
| 1 | 0,35 | 1,4 | 0,49 | 0,1225 | 1,96 | 0,686 | 0,1715 | 0,2401 | 5,9 |
| 1 | 0,35 | 1,6 | 0,56 | 0,1225 | 2,56 | 0,896 | 0,196 | 0,3136 | 6,1 |
| 1 | 0,35 | 1,8 | 0,63 | 0,1225 | 3,24 | 1,134 | 0,2205 | 0,3969 | 6,3 |
| 1 | 0,4 | 0,2 | 0,08 | 0,16 | 0,04 | 0,016 | 0,032 | 0,0064 | 1,2 |
| 1 | 0,4 | 0,4 | 0,16 | 0,16 | 0,16 | 0,064 | 0,064 | 0,0256 | 2,6 |
| 1 | 0,4 | 0,6 | 0,24 | 0,16 | 0,36 | 0,144 | 0,096 | 0,0576 | 3,8 |
| 1 | 0,4 | 0,8 | 0,32 | 0,16 | 0,64 | 0,256 | 0,128 | 0,1024 | 4,9 |
| 1 | 0,4 | 1 | 0,4 | 0,16 | 1 | 0,4 | 0,16 | 0,16 | 5,6 |
| 1 | 0,4 | 1,2 | 0,48 | 0,16 | 1,44 | 0,576 | 0,192 | 0,2304 | 6 |
| 1 | 0,4 | 1,4 | 0,56 | 0,16 | 1,96 | 0,784 | 0,224 | 0,3136 | 6,3 |
| 1 | 0,4 | 1,6 | 0,64 | 0,16 | 2,56 | 1,024 | 0,256 | 0,4096 | 6,6 |
Скористаємося цією таблицею для визначення функції відгуку, яка встановлює аналітичний зв’язок між ІК – параметром оптимізації і незалежними змінними ІБ , UКЕ – факторами. Для цього формуємо матрицю Х – вектор значення факторів, матрицю Y – відгук технічної системи. Далі знаходимо матрицю (ХТ · Х)-1 , яка називається матрицею похибок або матрицею коваріацій. Вона має наступний вигляд:
(ХТ * Х)-1
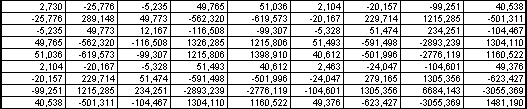
Рис. 2 Матриця коваріацій для моделі
Виходячи з отриманих даних знайдемо коефіцієнти поліному bi . Матриця коефіцієнтів В = (ХТ * Х)-1 * (ХT * Y) має вигляд (рис.3)
| B0 | 0,144 |
| B1 | 7,649 |
| B2 | -0,185 |
| B3 | 20,067 |
| B4 | -24,031 |
| B5 | -0,193 |
| B6 | -1,604 |
| B7 | 8,677 |
| B8 | -14,015 |
Рис. 3. Матриця коефіцієнтів В
Отже, математична модель залежності Iк (Uке , Іб ) буде представлена наступною функцією:
Y’ = 0,144+ 7,649Iб -0,185 Uке + 20,066Uке Iб – 24.0314Iб 2 – 0.193Uке 2 –
–1,604Uке 2 Iб + 8,677Iб 2 Uке – 14,015Uке 2 Iб 2