Контрольная работа: Область прогноза для однофакторной и двухфакторной модели. Точечный прогноз на основании линейной прогрессии
Подставляя в уравнение (2) значения из каждой строки таблицы, получим n уравнений.
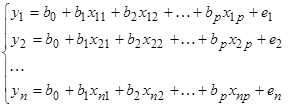 (2)
(2)
ei – случайные отклонения (остатки), наличие которых объясняется тем, что выборочные точки не ложатся в точности на плоскость (1), а случайным образом разбросаны вокруг нее.
![]()
Чтобы записать систему (2) в матричном виде, вводим матрицу X , составленную из множителей при коэффициентах b1 , b2 , …, bp .
Матрица 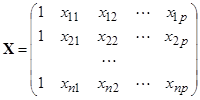 . Размерность матрицы n´p+1.
. Размерность матрицы n´p+1.
Еще вводятся матрицы:
Вектор столбец 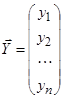 ,
, 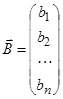 ,
, 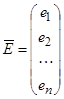 , размерностью n´1.
, размерностью n´1.
Тогда в матричной форме уравнение регрессии записывается так:
![]() .
.
Полуширина доверительного интервала рассчитывается по формуле:
![]() ,
,
где ![]() - среднее квадратическое отклонение остатков;
- среднее квадратическое отклонение остатков;
![]() - критическая точка распределения Стьюдента, соответствующая уровню доверия g=(0.95, 0.99, 0.999) и степени свободы k=n-p-1.
- критическая точка распределения Стьюдента, соответствующая уровню доверия g=(0.95, 0.99, 0.999) и степени свободы k=n-p-1.
вектор 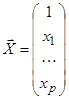 точка из области прогноза.
точка из области прогноза.
2. Задача
Найдите коэффициент эластичности для указанной модели в заданной точке x. Сделать экономический вывод.
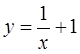
X=1
1. Найдем производную функции 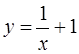 ,
,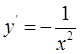
2. Найдем эластичность. ![]() , тогда
, тогда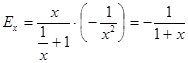
3. Коэффициент эластичности для точки прогноза:
X=1
![]()
Коэффициент эластичности показывает, что при изменении фактора X =1 на 1% показатель Y уменьшится на 0,5%.
3. Задача
Для представленных данных выполнить следующее задание:
1. Провести эконометрический анализ линейной зависимости показателя от первого фактора. Сделать прогноз для любой точки из области прогноза, построить доверительную область. Найти коэффициент эластичности в точке прогноза.
2. Провести эконометрический анализ нелинейной зависимости показателя от второго фактора, воспользовавшись подсказкой. Сделать прогноз для любой точки из области прогноза, построить доверительную область. Найти коэффициент эластичности в точке прогноза.