Контрольная работа: Область прогноза для однофакторной и двухфакторной модели. Точечный прогноз на основании линейной прогрессии

Коэффициент эластичности для точки прогноза:

Коэффициент эластичности показывает, что при изменении площади паши 15 % на 1% уровень убыточности животноводства увеличивается на 13.12%.

Обозначим удельный вес пашни – Х1 %, удельный вес лугов и пастбищ - Х2 %, уровень убыточности продукции животноводства - У %. Построим линейную зависимость показателя от факторов. Найдем основные числовые характеристики. Объем выборки n=15 – суммарное количество наблюдений. Минимальное значение Х1=68.1, максимальное значение Х1=94.7, значит, удельный вес пашни изменяется от 68.1 до 94.7%. Минимальное значение Х2=9.2, максимальное значение Х2=28.7, значит, вес лугов и пастбищ изменяется от 9.2 до 28.7%. Минимальное значение У=15, максимальное значение У=45.6, уровень убыточности животноводства изменяется от 15 до 45.6%. Среднее значение .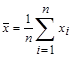

Среднее значение веса пашни составляет 80.98 %, среднее значение веса лугов и пастбищ составляет 17.02, среднее значение уровня убыточности животноводства составляет 28.17%.

Дисперсия =58,83, =42,45 =92.96%.

Среднеквадратическое отклонение 7.67, значит среднее отклонение веса пашни от среднего значения, составляет 7.67%., среднеквадратическое отклонение 6.52, значит среднее отклонение удельного веса лугов и пастбищ от среднего значения, составляет 6.52%,9.65, значит среднее отклонение уровня убыточного животноводства от среднего значения, составляет 9.65%.

Прежде чем строить модель, проверим факторы на коллинеарность. По исходным данным строим корреляционную матрицу. Коэффициент корреляции между X₁ и X₂ равен 0,89. Так как , значит X₁ и X₂ – неколлинеарные

Определим, связаны ли Х1, Х2 и У между собой.

Для определения тесноты линейной связи найдем коэффициент корреляции : r= 0,892. Так как то линейная связь между Х1, Х2 и У достаточная.

Пытаемся описать связь между х и у зависимостью.

Параметры b_0, b₁ ,b₂ находим по МНК. .

Проверим значимость коэффициентов b_i .

Значимость коэффициента b может быть проверена с помощью критерия Стьюдента:

-0,867. Значимость равна 0.402, т.е приблизительно 40%. Так как это значение намного больше 5%, то коэффициент b₀ статистически не значим.

3.04. Значимость равна 0.0102, т.е 1%. Так как это значение меньше 5%, то коэффициент b₁ статистически значим.

-2.107. Значимость равна 0.056, т.е 5%. Так как это значение больше 5%, то коэффициент b₂ статистически не значим.

Проверим адекватность.

Для анализа общего качества оцененной линейной регрессии найдем коэффициент детерминации: =0,8377. Разброс данных объясняется линейной моделью на 84% и на 16% – случайными ошибками. Качество модели хорошее.

Проверим с помощью критерия Фишера.

Для проверки найдем величины: 545.17 и 17.6. Вычисляем k₁ =2, k₂ =12. Находим наблюдаемое значение критерия Фишера 30.98 Значимость этого значения a=0.000018, т.е. процент ошибки равен 0,00018%. Так как это значение меньше 5%, то модель считается адекватной с гарантией более 99%.

Получили модель зависимости уровня удельного веса пашни от удельного веса лугов и пастбищ и убыточности скотоводства

Найдем прогноз на основании линейной регрессии. Выберем произвольную точку из области прогноза: х1=80, х2=30. Рассчитываем прогнозные значения по модели для всех точек выборки и для точки прогноза:

Т.е. при удельном весе пашен 80% и весе лугов и пастбищ 30% уровень убыточности животноводства составит 19.86%.

Найдем эластичность по каждому фактору.

Для линейной модели

,