Контрольная работа: Область прогноза для однофакторной и двухфакторной модели. Точечный прогноз на основании линейной прогрессии
Выполнил:
студент гр. ПВ 09-1з
Измайлов А.О.
Проверила:
Гетьман И.
Краматорск 2010
1. Теоретический вопрос
Область прогноза для однофакторной и двухфакторной модели. Точечный прогноз на основании линейной прогрессии.
Область прогнозов находится так: среди выборочных х находят xmin и xmax . Отрезок прямой, заключенный между ними называется областью прогнозов.
 |
Прогнозируемый доверительный интервал для любого х такой ![]() .
.
Совокупность доверительных интервалов для всех х из области прогнозов образует доверительную область, которая представляет область заключения между двумя гиперболами. Наиболее узкое место в точке ![]() .
.
 |
Прогноз для произвольного х дает интервал, в который с вероятностью g попадает неизвестное ![]() . Т.е. прогноз при заданном х составит от
. Т.е. прогноз при заданном х составит от ![]() до
до ![]() с гарантией
с гарантией ![]() .
.
Максимальная ошибка прогноза.
Выборочные значения yi равны ![]() , где
, где ![]() коэффициенты регрессии для всей генеральной совокупности,
коэффициенты регрессии для всей генеральной совокупности, ![]() - случайная величина, значение которой мы определить не можем, так как не знаем
- случайная величина, значение которой мы определить не можем, так как не знаем ![]() .
.
Для неизвестных коэффициентов ![]() могут быть найдены доверительные интервалы, в которые с надежностью g попадают
могут быть найдены доверительные интервалы, в которые с надежностью g попадают ![]() :
: ![]() ,
, ![]() .
.
Геометрический смысл коэффициента ![]() - ордината пересечения прямой регрессии с осью 0Y, коэффициента
- ордината пересечения прямой регрессии с осью 0Y, коэффициента ![]() - угловой коэффициент прямой регрессии. Вследствие этого возникает следующая ситуация:
- угловой коэффициент прямой регрессии. Вследствие этого возникает следующая ситуация:

Истинная прямая регрессии может с вероятностью g занимать любое положение в доверительной области.
Наиболее максимальное отклонение от расчетного значения - ![]() или
или ![]() . Найдем ошибку прогноза для каждого из значений:
. Найдем ошибку прогноза для каждого из значений:
![]() ,
, ![]() .
.
Т.е. максимальная ошибка прогноза в процентах составляет: ![]() , т.е. чем больше полуширина доверительного интервала, тем больше ошибка. Ширина доверительного интервала возрастает с ростом коэффициента доверия и уменьшается с ростом объема выборки со скоростью
, т.е. чем больше полуширина доверительного интервала, тем больше ошибка. Ширина доверительного интервала возрастает с ростом коэффициента доверия и уменьшается с ростом объема выборки со скоростью ![]() . Т.е. увеличив объем выборки в 4 раза, в 2 раза сузим доверительный интервал, т.е. в 2 раза уменьшим ошибку прогноза. С уменьшением коэффициента доверия уменьшается ошибка прогноза, но растет вероятность того, что истинное значение не попадет в доверительный интервал.
. Т.е. увеличив объем выборки в 4 раза, в 2 раза сузим доверительный интервал, т.е. в 2 раза уменьшим ошибку прогноза. С уменьшением коэффициента доверия уменьшается ошибка прогноза, но растет вероятность того, что истинное значение не попадет в доверительный интервал.
Прогноз на основании линейной модели для двуфакторной модели.
Целью регрессионного анализа является получение прогноза с доверительным интервалом. Прогноз делается по уравнению регрессии
![]() (1)
(1)
Точка прогноза ![]() из p -мерного пространства с координатами
из p -мерного пространства с координатами ![]() выбирается из области прогноза. Если, например, модель двухфакторная
выбирается из области прогноза. Если, например, модель двухфакторная ![]() , то область прогноза определяется прямоугольником, представленным на рис. 1.
, то область прогноза определяется прямоугольником, представленным на рис. 1.
 |
Рис. 1
Т.е. область прогноза определяется системой неравенств:
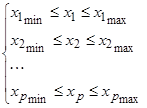
Чтобы получить формулу для вычисления полуширины d доверительного интервала, нужно перейти к матричной форме записи уравнения регрессии.
Матричная запись многофакторной регрессии
Данные для построения уравнения регрессии, сведем в таблицу:
Таблица 1
| № набл | Y | X1 | X2 | … | Xp |
| 1 | y1 | x11 | x12 | x1p | |
| 2 | y2 | x21 | x22 | x2p | |
| … | |||||
| n | yn | xn1 | xn2 | xnp |
--> ЧИТАТЬ ПОЛНОСТЬЮ <--