Контрольная работа: Определение устойчивости равновесия Расчет зависимости напряженности электрического поля от

Два положительных точечных заряда и закреплены на расстоянии друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещение зарядов возможны только вдоль прямой, проходящей через закрепленные заряды.

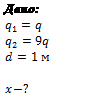
Решение:

Определим знак заряда, при котором равновесие будет устойчивым.

Если заряд отрицательный, то при смещении его влево сила (направленная влево) возрастает, а сила (направленная вправо) возрастает. Под действием этой силы заряд удаляется от положения равновесия. То же происходит и при смещении заряда вправо. Равновесие будет неустойчивым.

Если заряд положителен, то при смещении его влево сила (направленная вправо) возрастает, а сила (направленная влево) убывает, следовательно, результирующая сила будет направлена вправо и заряд возвращается к положению равновесия. То же происходит и при смещении заряда вправо. Равновесие будет устойчивым.

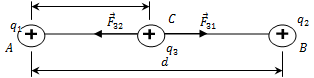
Предположим, что заряд находится в точке . Тогда условие равновесия заряда запишется так:

Подставив в уравнение вместо сил их значения по закону Кулона, и произведя сокращения, получим:

Решая относительно , получаем:

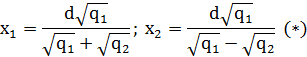
Так как –эта точка расположена вне отрезка , что невозможно для равновесия заряда .

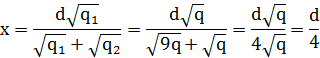
Произведем вычисления:

Ответ: положительный.

322

На двух концентрических сферах радиусом и равномерно распределены заряды с поверхностными плотностями и соответственно. Используя теорему Гаусса, найти зависимость напряженности электрического поля от расстояния для трех областей: и . Принять , . 2) вычислить напряженность в точке, удаленной от центра на расстояние и указать направление вектора для значений , . 3) построить график .

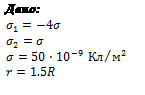
Решение:

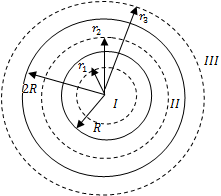
1) Для определения напряженности в области проведем гауссову поверхность радиусом .

По теореме Остроградского –Гаусса имеем:

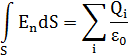
Для области : -заряда внутри сферы нет

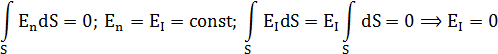
Напряженность поля в области равна нулю.

Для области проведем гауссову поверхность радиуса :

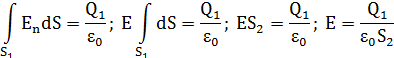
Площадь гауссовой поверхности:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--