Контрольная работа: Определение вероятности

КОНТРОЛЬНАЯ РАБОТА № 11

ВАРИАНТ 8

1. В ящике 10 деталей, среди которых 3 бракованных. Случайно извлекли 4 детали. Найти вероятность того, что среди них окажутся две бракованных.

Будем использовать классическое определение вероятности.

Четыре детали из десяти можно выбрать способами (число сочетаний из десяти элементов по четыре). Поэтому n — число равновозможных событий равно т.к.

Две бракованных детали из трех можно выбрать способами:

Две стандартных детали из семи можно выбрать способами:

,

поэтому m — число благоприятных событий равно .

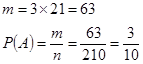
2. ОТК проверяет изделие на стандартность. Вероятность стандартности изделия равна 0,85. Найти вероятность того, что из двух проверенных изделий только одно стандартно. Ответ записать в виде десятичной дроби.

Введем события — первое проверенное изделие стандартное, — второе проверенное изделие стандартное, — первое проверенное изделие нестандартное, — второе изделие нестандартное, — из двух проверенных изделий только одно стандартное. Тогда . События несовместимы, поэтому по правилу сложения вероятностей , получаем: , т.к. события и — независимы, то .

По условию:

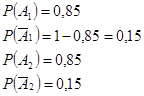
Получаем:

3. Три стрелка А, В, С стреляют по некоторой цели, делая не более одного выстрела. Вероятности попадания их при одном выстреле соответственно равны 0,7, 0,8, 0,9. Стрельбу начинает А. Если он промахнется, то стреляет в. Если и В промахнется, то стреляет С. Найти вероятность (в виде десятичной дроби) того, что цель будет поражена.

Пусть событие — цель поражена, гипотезы: — первый стрелок попал в цель, — первый стрелок промахнулся, второй попал, — первый промахнулся, второй промахнулся, третий попал.

Вероятность события :

.

По формуле умножения вероятностей ( учитывая, что вероятности промаха стрелками равен соответственно ).

По формуле сложения вероятностей получим:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--