Контрольная работа: Основные задачи вычислительной математики
Определение: предельной относительной погрешностью ![]() данного приближённого числа
данного приближённого числа ![]() называется всякое число, не меньшее относительной погрешности этого числа:
называется всякое число, не меньшее относительной погрешности этого числа:
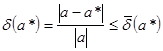 (1.7)
(1.7)
Отсюда следует, что
![]() (1.8)
(1.8)
т.е.
![]() (1.9)
(1.9)
но, как известно:
![]() (1.10)
(1.10)
Сопоставление формул (1.9) и (1.10) даёт соотношение между предельной абсолютной ![]() погрешностью и предельной относительной погрешностью
погрешностью и предельной относительной погрешностью ![]() :
:
![]() (1.11)
(1.11)
Из этой формулы иногда выражают ![]() и пишут:
и пишут:
![]() (1.12)
(1.12)
Рассмотрим примеры:
Пример 3: Вес 1 дм3 воды при ![]() равен
равен ![]() г. Определить предельную относительную погрешность результата взвешивания.
г. Определить предельную относительную погрешность результата взвешивания.
Решение: очевидно, что предельная абсолютная погрешность ![]() г. и
г. и ![]() , следовательно:
, следовательно:
![]() (1.13)
(1.13)
Пример 4: При определении газовой постоянной для воздуха, получили ![]() . Зная, что относительная погрешность этого значения
. Зная, что относительная погрешность этого значения ![]() , найти пределы, в которых заключается R.
, найти пределы, в которых заключается R.
Решение: имеем: ![]() , тогда
, тогда ![]() , т.е.
, т.е.
![]() (1.14)
(1.14)
Теперь займёмся изучением распространения погрешностей из-за арифметических действий.
б) Рассмотрим функцию ![]() , пусть значения переменных
, пусть значения переменных ![]() , вычислены приближённо, где
, вычислены приближённо, где ![]() соответствующие абсолютные погрешности.
соответствующие абсолютные погрешности.
Нас интересует абсолютная и относительная погрешности вычисленных значений функции ![]() .
.
По определению видно, что абсолютная погрешность функции ![]() имеет вид:
имеет вид:
![]()
обычно ![]() , поэтому, раскладывая в ряд Тейлора, можно ограничиться лишь линейными членами по
, поэтому, раскладывая в ряд Тейлора, можно ограничиться лишь линейными членами по ![]() . Получаем:
. Получаем:
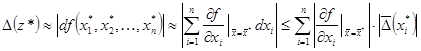 (1.15)
(1.15)
Отсюда получаем оценку:
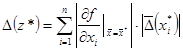 (1.16)
(1.16)
Тогда для предельных абсолютных погрешностей имеем: