Контрольная работа: Показатели эконометрики

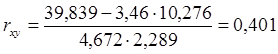
r_xy = 0,401, 0,3≤0,401≤0,5 – связь слабая

Коэффициент детерминации R = r_xy ² ∙100% = 0,401² ∙100% = 16,08.

y зависит от выбранного x на 16,08%, на оставшиеся 100-16,08% y зависит от других факторов.

Оценим статистическую значимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдента.

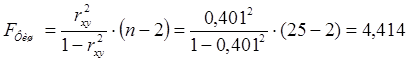
Приα = 0,05, κ₁ = n-1, κ₂ = n-2 =25-2 =23

F_{табл .} = 2,00, F_Фиш. = 4,414 > F_табл. = 2,00 – модель значима и надежна

Рассчитаем прогнозное значение результата с вероятностью 0,95% при повышении дозы внесения удобрений от своего среднего уровня и определим доверительный интервал прогноза.

Найдем точечный прогноз для х_{прогноз} = 1,2∙х , х_р = 1,2 ∙3,46 = 4,152

ỹ = a + bx , ỹ_р = 9,598 + 0,196∙ х_р = 9,598 + 0,196∙4,152 = 10,412

Найдем среднюю ошибку прогнозного значения

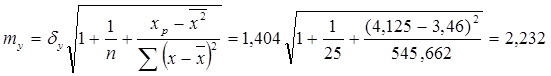
F_табл. Стьюдента для α = 0,05, df = n-2 = 25-2 = 23

t_табл. =2,0687,

∆_ур = t_табл ∙станд.ошибка = 2,0687∙2,188 = 4,526

Доверительный интервал прогноза по урожайности

γ_ур = y_p ± ∆_ур = 10,412 ± 4,526, от 5,886 до 14,938

Таблица 1. Исходные данные для задачи 1

№	Внесено мин.удобрений, ц	Урожайность, ц/га	Х2	у∙х	У2	Урожайность расчетная,Ỹ	(Y-Ỹ)	(Y-Ỹ)/100	(Y-Ỹ)2	(Х-¯Х)2
1	13,9	9,4	193,21	130,66	88,36	12,322	-2,922	31,085	8,538	108,994
2	8,8	15	77,44	132	225	11,323	3,677	100,245	13,52	28,516
3	4	8,2	16	32,8	67,24	10,382	-2,182	26,610	4,761	0,292
4	0,01	8,2	0,0001	0,082	67,24	9,6	-1,4	17,073	1,96	11,903
5	4,2	13,7	17,64	57,54	187,69	10,421	3,279	23,934	10,752	0,548
6	0,7	9,2	0,49	6,44	84,64	9,735	-0,535	5,815	0,286	7,618
7	6,7	12,4	44,89	83,08	153,76	10,911	1,489	12,008	2,217	10,498
8	15,9	14	252,81	222,6	196	12,714	1,286	9,186	1,654	154,754
9	1,9	8,6	3,61	16,34	73,96	9,97	-1,37	15,930	1,877	2,434
10	1,9	14,7	3,61	27,93	216,09	9,97	4,73	32,177	22,373	2,434
11	0,01	6,3	0,0001	0,063	39,69	9,6	-3,3	52,381	10,89	11,903
12	0,01	8,5	0,0001	0,085	72,25	9,6	-1,1	12,941	1,21	11,903
13	0,01	8,8	0,0001	0,088	77,44	9,6	-0,8	9,091	0,64	11,903
14	1,2	10,9	1,44	13,08	118,81	9,833	1,067	9,789	1,138	5,108
15	0,01	9,2	0,0001	0,092	84,64	9,6	-0,4	4,348	0,16	11,903
16	0,01	13,4	0,0001	0,134	179,56	9,6	3,8	28,358	14,44	11,903
17	3,7	10,8	13,69	39,69	116,64	10,323	0,477	4,417	0,288	0,058
18	0,01	7,9	0,0001	0,079	62,41	9,6	-1,7	21,519	2,89	11,903
19	0,01	9,1	0,0001	0,091	82,81	9,6	-0,5	5,495	0,25	11,903
20	1,6	9,2	2,56	14,72	84,64	9,912	-0,712	7,739	0,507	3,460
21	2,5	10,3	6,25	25,75	106,09	10,088	0,212	2,058	0,045	0,922
22	0,01	11,1	0,0001	0,111	123,21	9,6	1,5	13,514	2,25	11,903
23	6,3	9,5	39,69	59,85	90,25	10,833	-1,333	14,032	1,777	8,066
24	0,01	8,4	0,0001	0,084	70,56	9,6	-1,2	14,286	1,44	11,903
25	13,1	10,1	171,61	132,31	102,01	12,166	-2,066	20,455	4,268	92,930
Итого	86,5	256,9	844,941	995,969	2770,99	256,903	0,003	494,486	110,071	545,662
Среднее значение	3,46	10,276	33,798	39,839	110,84	21,826

Задача 2

По данным представленным в таблице 3 изучается зависимость бонитировочного балла (У) от трех факторов.

С помощью ППП MSExcel:

1. Построить матрицу парных коэффициентов корреляции. Установить, какие факторы мультиколлинеарны.

2. Построить уравнение множественной регрессии в линейной форме с полным набором факторов.

3. Оценить статистическую значимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдента.

4. Отобрать информативные факторы. Построить уравнение регрессии со статитически значимыми факторами.