Контрольная работа: Послідовність незалежних випробувань
Якщо перетворити праву частину функції і звести подібні члени, то коефіцієнт при ![]() визначає
визначає![]()
У теорії ймовірностей часто застосовуються деякі закони розподілу випадкових величин. Розглянемо ці розподіли, а також задачі, де вони використовуються.
Біноміальний закон розподілу
Імовірності в цьому законі визначаються за формулою
![]()
![]()
m = 0,1,2, …, n .
Закон справджується для схеми незалежних повторних випробувань, у кожному з яких подія А настає з імовірністю р . Частота настання події А має біноміальний закон розподілу. Числові характеристики розподілу:
![]()
2. Оцінка дисперсії
Оцінка параметра розподілу сукупності ![]() у загальному випадку є випадковою величиною, яка визначається за даними вибірки і використовується замість невідомого значення параметра, який потрібно оцінити.
у загальному випадку є випадковою величиною, яка визначається за даними вибірки і використовується замість невідомого значення параметра, який потрібно оцінити.
Оцінка називається обґрунтованою , якщо вона збігається за ймовірністю до відповідного параметра при ![]()
Оцінка називається незміщеною , якщо її математичне сподівання збігається зі значенням параметра.
У різі вибору з усіх відомих незміщених обґрунтованих оцінок певної оцінки потрібно зазначити критерій, за яким зроблено вибір.
Найчастіше застосовується критерій, який полягає у виборі оцінки, що має найменшу можливу дисперсію. Така оцінка називається ефективною . Нижня межа дисперсії незміщеної оцінки параметра ![]() (яку позначатимемо
(яку позначатимемо ![]() ), подається формулою:
), подається формулою:
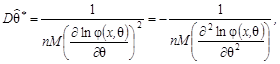
де ![]() — щільність розподілу випадкової величини (для дискретної випадкової величини
— щільність розподілу випадкової величини (для дискретної випадкової величини ![]() ).
).
Оцінки параметрів розподілу знаходять методами максимальної правдоподібності і моментів. Метод максимальної правдоподібності полягає ось у чому. Нехай закон розподілу випадкової величини подається через параметр ![]() , який у загальному випадку k -вимірний. Тоді для вибірки
, який у загальному випадку k -вимірний. Тоді для вибірки ![]() спільний закон розподілу подається функцією правдоподібності (запишемо, наприклад, для неперервних величин):
спільний закон розподілу подається функцією правдоподібності (запишемо, наприклад, для неперервних величин):
![]()
За оцінки максимальної правдоподібності параметрів ![]() беруться вибіркові функції, які є розв’язком системи рівнянь:
беруться вибіркові функції, які є розв’язком системи рівнянь:
![]()
Застосування методу моментів ґрунтується на збіжності (за ймовірністю) статистичних моментів розподілу до відповідних теоретичних моментів розподілу, які в такому разі мають існувати. Як відомо, теоретичні моменти розподілу виражаються через параметри розподілу. Складаємо систему k рівнянь, в якій попарно прирівнюємо відповідні теоретичні і статистичні моменти. Розв’язком цієї системи є оцінки для параметрів розподілу.
Нехай маємо точкову оцінку ![]() параметра
параметра ![]() . Знайдемо для параметра інтервальну оцінку, скориставшись умовою
. Знайдемо для параметра інтервальну оцінку, скориставшись умовою ![]() В такому разі e називається точністю оцінки , а g — її надій- ністю . Тоді інтервальна оцінка (довірчий інтервал) для параметра q набуває вигляду
В такому разі e називається точністю оцінки , а g — її надій- ністю . Тоді інтервальна оцінка (довірчий інтервал) для параметра q набуває вигляду ![]() Параметр q — не випадкова величина, надійність g можна розглядати як імовірність того, що випадковий інтервал покриває дійсне значення параметра. Величини
Параметр q — не випадкова величина, надійність g можна розглядати як імовірність того, що випадковий інтервал покриває дійсне значення параметра. Величини ![]() тісно зв’язані з обсягом вибірки
тісно зв’язані з обсягом вибірки ![]() Якщо задати дві з цих величин, то можна знайти третю. Для цього потрібно знати закон розподілу для
Якщо задати дві з цих величин, то можна знайти третю. Для цього потрібно знати закон розподілу для ![]()
Приклади розв’язування задач
Приклад 1 . Вибірку обсягом n зроблено із сукупності, розподіленої за законом Релея
![]()
Знайти оцінку для параметра ![]() і перевірити її на незміщеність, обґрунтованість і ефективність.
і перевірити її на незміщеність, обґрунтованість і ефективність.
Розв’язання. Застосуємо метод максимальної правдоподібності. Побудуємо функцію правдоподібності, складемо і розв’я жемо рівняння для визначення оцінки:
![]()
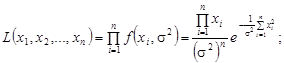
![]()
![]()
![]()
Перевіримо оцінку на незміщеність, знайшовши її математичне сподівання: