Контрольная работа: Послідовність незалежних випробувань
Перетворення виконано згідно з властивостями математичного сподівання та з урахуванням того, що результати вибірки є незалежними однаково розподіленими випадковими величинами. Знайдемо ![]() випадкової величини, розподіленої за законом Релея:
випадкової величини, розподіленої за законом Релея:
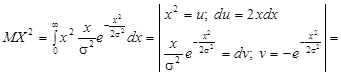
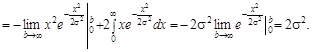
Тоді ![]() тобто оцінка незміщена.
тобто оцінка незміщена.
Перевірку обґрунтованості оцінки виконаємо, скориставшись другою формою нерівності Чебишова, тобто оцінимо ймовірність ![]() Щоб знайти дисперсію оцінки, виконаємо обчислення:
Щоб знайти дисперсію оцінки, виконаємо обчислення:
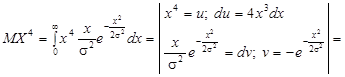
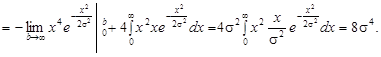
(Останній інтеграл, що є математичним сподіванням квадрата випадкової величини, дорівнює ![]() і обчислювався раніше.) Тоді
і обчислювався раніше.) Тоді ![]() Отже, маємо:
Отже, маємо:
![]()
Підставляючи дисперсію оцінки в нерівність Чебишова, дістаємо:
![]()
Отже, оцінка обґрунтована.
Знаходимо дисперсію ефективної оцінки:
![]()
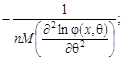
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Дисперсія ефективної оцінки збігається з дисперсією знайденої оцінки для ![]() а це означає, що оцінка ефективна.
а це означає, що оцінка ефективна.
Приклад 2 . За методом моментів знайти оцінку параметра р геометричного розподілу за даними вибірки обсягом n .
Розв’язання. Геометричний закон розподілу визначається формулою:
![]()
Оскільки потрібно знайти оцінку одного параметра, зрівнюємо теоретичні і статистичні початкові моменти першого порядку:
![]()
Приклад 3 . За даними вибірки обсягом n із нормально розподіленої сукупності, дисперсія якої ![]() , а надійність
, а надійність ![]() , знайти інтервальну оцінку для математичного сподівання цієї сукупності.
, знайти інтервальну оцінку для математичного сподівання цієї сукупності.
Розв’язання. Інтервальна оцінка для математичного сподівання, якщо дисперсія сукупності ![]() відома, подається у вигляді
відома, подається у вигляді
![]() де
де ![]()
![]() де
де ![]() — функція Лапласа.
— функція Лапласа.
Для побудови оцінки розглядалась вибіркова функція ![]() яка має нормальний закон розподілу з нульовим математичним сподіванням і одиничною дисперсією.
яка має нормальний закон розподілу з нульовим математичним сподіванням і одиничною дисперсією.
Приклад 4 . Розв’язати попередню задачу для випадку, коли дисперсія сукупності невідома.
Розв’язання. У цьому випадку інтервальну оцінку побудуємо за допомогою вибіркової функції
![]()
яка розподілена за законом Стьюдента з n – 1 ступенями волі. Довірчий інтервал
![]()
де ![]() а
а ![]() де
де ![]() — функція розподілу Стьюдента з n – 1 ступенями волі. Якщо кількість ступенів волі перевищує 20, то розподіл Стьюдента практично не відрізняється від нормального закону розподілу з нульовим математичним сподіванням і одиничною дисперсією.
— функція розподілу Стьюдента з n – 1 ступенями волі. Якщо кількість ступенів волі перевищує 20, то розподіл Стьюдента практично не відрізняється від нормального закону розподілу з нульовим математичним сподіванням і одиничною дисперсією.
Приклад 5 . За результатами вибірки обсягом n із нормально розподіленої сукупності з надійністю ![]() знайти довірчий інтервал для дисперсії сукупності.
знайти довірчий інтервал для дисперсії сукупності.