Контрольная работа: Построение двухфакторной модели, моделей парной линейной прогрессии и множественной линейной регрессии
ЗАДАНИЕ № 2
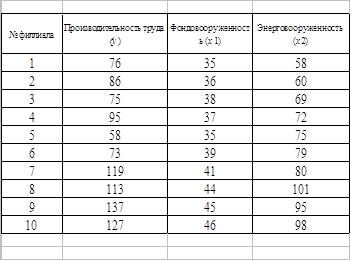
Результаты обследования десяти статистически однородных филиалов фирмы в таблице (цифры условные). Требуется:
А. Построить модель парной линейной прогрессии производительности труда от фактора фондовооруженности, определить коэффициент регрессии, рассчитать парный коэффициент корреляции, оценить тесноту корреляционной связи, найти коэффициент эластичности и бета – коэффициент: пояснить экономический смысл всех коэффициентов;
Б. Построить модель множественной линейной регрессии производительности труда от факторов фондо- и энерго- вооруженности, найти все коэффициенты корреляции и детерминации, коэффициенты эластичности и - коэффициенты, пояснить экономический смысл всех коэффициентов.
Решение
А. Обозначим производительность труда через у – резтивный признак, два других признака фондовооруженость и энерговооруженность будут фак.х1 и х2. Рассмотрим линейную модель зависимости производительности труда – у от величины фондовооруженности – х 1 это модель выражения линейной функции f вида у = а0 + а1*х1, параметры которой находят в результате решения системы нормального уровня, сформированных на основе метода наименьших квадратов, суть которого заключается в то, что бы сумма квадратов отклонений фактических уравнений ряда от соответствующих, выровненных по кривой роста значений была наименьшей.
![]() а0*n+а_х1=_у
а0*n+а_х1=_у
а0*_х1+а1*_х1^2=_(у*х1),
где суммирование приводится по всем
- n- группам,
- параметры а 0 и а 1можно рассчитать по формуле:
![]() а 1= cov (х1*у) = ух 1-ух 1
а 1= cov (х1*у) = ух 1-ух 1
var (х1) х 2-2/х 1
а 0 = у -а 1*х
![]() 10*а 0+396*а 1 = 959
10*а 0+396*а 1 = 959
396*а 0+15838*а 1 = 38856
Составим расчетную таблицу
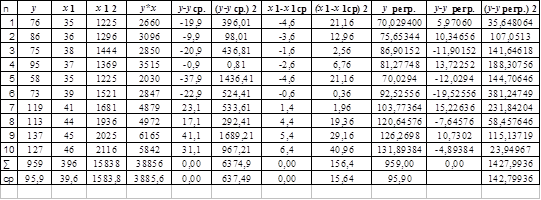
Из расчета таблицы имеем
ух 1 = 3885,60
х 1 = 1583,80
Дополнительно рассчитываем
ух 1 = 95,9*39,6 = 3797,64
х 1 = (39,6)^2 = 1568.16
а 1 = 3885,6-3797,64 = 87,96 = 5,624040
1583,8-1568,16 15,64
а 0 = 95,9-5,624040*39,6 = -126,81,
таким образом однофакторная модель имеет вид: