Контрольная работа: Построение двухфакторной модели, моделей парной линейной прогрессии и множественной линейной регрессии
ЗАДАНИЕ №1
По предложенной выборке наблюдений результативного признака у и факторных признаков х1,х2,х3 требуется с помощью корреляционного анализа выбрать факторные признаки для построения двухфакторной модели и пояснить свой выбор.
| n | у | х1 | х2 | х3 |
| 1 | 88 | 38 | 54 | 87 |
| 2 | 71 | 49 | 92 | 57 |
| 3 | 62 | 44 | 74 | 68 |
| 4 | 49 | 78 | 76 | 42 |
| 5 | 76 | 62 | 41 | 76 |
Решение
Для получения искомых величин составим расчетную таблицу:
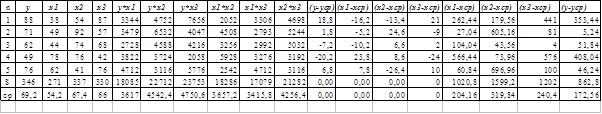
Получим: x1 = 54,2, х2=67,4, х3= 66; у*х1=3617; у*х2=4542,4; у*х3=4750,6; х1*х2=3657,2; х1*х3=3415,8; х2*х3= 4256,4
Рассчитаем r коэффициент корреляции между величинами у и х1; у и х2; у и х3; х1 и х2; х2 и х3; х1 и х3;
Cov ( x *у)= х*у –х*у
Cov ( x 1*у)=3617-54.2*69.2 =-133,64
Cov ( x 2*у)=4542,4-67,4*69,2 =-121,68
Cov ( x 3*у)=4750,6-66*69,2 =183,4
Rх1у = cov(х1;у) = -133,64 = -133,64 =- 0,712
Var ( x 1) Var ( y ) 204,16*172,56 187,696
Rх2у = cov(х2;у) =-121,68 = -121,68 = -0,5179
Var ( x 2) Var ( y ) 319,84*172,56 234,928
R х3у = cov (х3;у) =183,4 =183,4 = 0,900
Var ( x 3) Var ( y ) 240,4*172,56 203,675
Cov (x1*x2)=x1*x2-x1*x
Cov(x1*x2)=3657,2-54,2*67,4=4,12
Cov(x1*x3)=3415,8-54,2*66=-161,4
Cov(x2*x3)==4256,4-67,4*66=-192
Rх1х2 = cov(х1;х2)=4,12= 4,12 = 0,016
Var ( x 1) Var (х2) 204,16*319,84 255,5357
R х1х3 = cov (х1;х3) = -161,4 = -161,4 = -0,728
Var (х1) Var (х3) 204,16*240,4 221,54
R х2х3 = cov (х2;х3) = -192 = -192 = -0,692
Var (х2) Var (х3) 240,4*319,84 277,288
Построим расчетную таблицу для двухфакторной модели
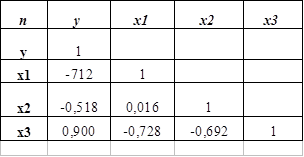
--> ЧИТАТЬ ПОЛНОСТЬЮ <--