Контрольная работа: Построение двухфакторной модели, моделей парной линейной прогрессии и множественной линейной регрессии
у регр = -126,812+5624041*х 1
Полученное уравнение является уравнением парной регрессии, коэффициента а 1 в этом уравнении называется коэффициентом регрессии. Знак этого коэффициента определяется направлением связи между у и х 2. В нашем случае эта связь образуется а 1 = +5,624040(+) – связь прямая.
Теснота связи между у и х1 определяется коэффициентом корреляции:
rух1 = V1-о у регр.^ 2/ оу^2 , где оу – средняя квадратная ошибка выборки у из значений таблицы
| rух1 | 0.8809071 |
rух1 = V1-142.79937/637.49 = 0.8809071
Чем ближе коэффициент корреляции к единице, тем теснее корреляционная связь: rух1=0,881, следовательно, связь между производительностью труда и фондовооруженностью достаточно тесная.
Коэффициент детерминации rух1^2
| rух1^2 | 0.7759974 |
Это означает, что фактором фондовооруженности можно объяснить 77,6% изменения производительности труда.
Коэффициент эластичности Эух1 = а1*х1 ср./ у ср.; Эух1 = 5,624040*39,6/95,9
| Эух1 | 2,322336 |
Это означает, что при увеличении фондовооруженности на 1%, производительность труда увеличится на 2,3223%.
Бета коэффициент _ух1 = а1*ох1/оу,
_ух1 = 5,624040*V15.64/ V637,49 = 0,8809072
| _ух1 | 0,8809072 |
Это значит, что увеличение фондовооруженности на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего значения производительности труда на 0,88 среднеквадратического отклонения.
Б. Модуль множественных регрессий рассматривается на периметре двухфакторной линейной модели, отражающей зависимость производительности труда у, от величины фондовооруженности (х 1) и энерговооруженности (х 2), модуль множественной регрессии имеет вид у = а 0+а 1у 1+а 2х 2.Параметры модели а 0,а 1,а 2, находятся путем решения системы нормальных уравнений:
а 0*n +а 1*Sх 1+а 2*Sх 2=Sу
а 0*Sх 1+а 1* Sх 1^2+а 2*S(х 1*х 2) = S(у*х 1)
а 0*Sх 2+а 1*S(х 1*х 2)+а2*Sх 2^2 = Sу *х 2)
10*а 0+396*а 1+787*а 2 = 959
396*а 0+15838*а 1+31689*а 2 = 38859
787*а 0+31689*а 1+64005*а 2 = 78094
Рассчитаем таблицу
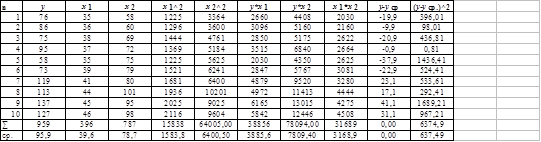
Решаем систему нормальным уравнением,методом Гаусса (метод исключения неизвестных).
Разделим каждое уравнение системы на коэффициент при а 0 соответственно:
а 0+39,6*а 1+78,7*а 2 = 95,9
а 0+39,994949*а 1+80,022727*а 2 = 98,128787
а 0+40,26556*а 1+81,327827*а 2 = 99,229987
из первогоуравнения системы вычитаем второе уравнение системы