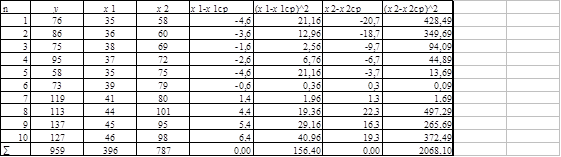Контрольная работа: Построение двухфакторной модели, моделей парной линейной прогрессии и множественной линейной регрессии

а 0 +39,994949а 1+30,022727а 2 = 98,128787

-0,394949-1,322727 = -2,228787

Из первого вычитаем третье уравнение:

а 0+39,6а +78,7а 2 = 95,9

а 0+40,26556*а 1+81,327827*а 2 = 99,229987

-0,665563-2,627827 = -3,329987

получим систему с двумя неизвестными

0,394949*а 1+1,322727а 2 = 2,228787

0,665565*а 1+2,627827а 2 = 3,329987

Делим каждое уравнение на β при а 1 соответственно:

а 1+3,349108а 2 = 5,643227

а 1+3,948265а 2 = 5,003248

из первого вычитаем второе

-0,599157а 2 = 0,639979

а 2 = -1,0681323

Полученное значение а 2 подставим в уравнение с двумя неизвестными:

а 1+3,349108а 2 = 5,643227

а 1 = 5,643227-3,349108*(-1,0681323)

а 1 = 5,643227+3,577290

а 1 =9,220517

Полученное значение а 1 и а 2 подставим в любое из уравнений с тремя неизвестными

а 0+39,6а +78,7а 2 = 95,9

а 0 = 95,9-39,6 а 1-78,7 а 2

а 0 = 95,9-39,6*9,220517-78,7*(-1,0681323)

а 0 = 95,9-365,132473+84,062012

а 0 = 185,170461

а 0 = -185,170461

Получим модель:

у = а 0+а 1х 1+а 2х 2

у = -185,170461+9,220517х 1-1,0681323х 2

Ответ: у = -185,170461+9,220517х 1-1,0681323х 2