Контрольная работа: Построение эпюр нормальных и касательных напряжений

Из эпюры изгибающих моментов:

M_max = 48,22 т · м = 48,22 · 10⁴ Н · м – максимальный изгибающий момент.

[σ] = 650 МПа – допускаемое нормальное напряжение для стали 40.

Требуемый осевой момент сопротивления изгибу из условия прочности:

W_тр ≥ |M_max | / [σ] = (48,22 · 10⁴ ) / 650 · 10⁶ = 0,074 · 10^-2 м³

Исследуем поперечные сечения различных форм (двутавр, швеллер, прямоугольник, квадрат, круг, треугольник)

Круг:

W_кр = πd³ / 32 = W_тр

d = = = 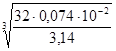0,2 м

S_кр = πd² / 4 = (3,14 · 0,2² ) / 4 = 0,0314 м² = 314 см² – площадь поперечного сечения.

Квадрат:

W_к = b³ / 6 = W_тр

d = = = 0,16 м

S_к = b² = 0,16² = 0,0256 м² = 256 см² – площадь поперечного сечения.

Прямоугольник:

W_п = ba² / 6 = W_тр ; a > b; возьмем a = 2b.

W_тр = 4b³ / 6; b = = = 0,1 м; a = 2 · 0,1 = 0,2 м

S_п = аb = 0,1 · 0,2 = 0,02 м² = 200 см² – площадь поперечного сечения.

Треугольник. При вычислении напряжения в вершине треугольника.

W_т = bh² / 24 = W_тр ; b – сторона треугольника, h – высота.

Возьмем: h = b /

W_тр = b³ / 48; b = = = 0,33 м; h = 0,33 / = 0,23 м

S_тр = 0,5hb = 0,5 · 0,33 · 0,23 = 0,038 м² = 380 см² – площадь поперечного сечения.

Швеллер.

По справочникам определим швеллер.

Берем швеллер №40. W_x = 761 cм³ ; h = 0,4 м; b = 0,115 м.

S_ш = 61,5 см² – площадь поперечного сечения.

Двутавр.

По справочникам определим двутавр.