Контрольная работа: Построение и анализ функции спроса на товар
Уравнение регрессии имеет вид:
ŷ = 87,927 + 0,1513х ,
Сравним фактические и расчетные расходы на потребление товара А (таблица 2) и построим график полученной функции ŷ (рисунок 1).
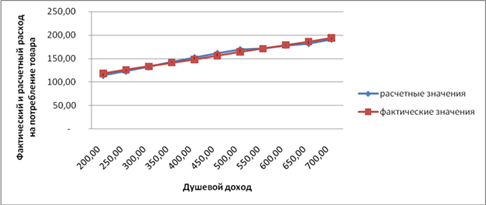
Рисунок 1 - Сравнение фактических и расчетных расходов на потребление товара А для линейного уравнения регрессии
По формуле ŷ = a + b х (2) (где, а - регрессионная постоянная, точка пересечения линии регрессии с осью OY , b - коэффициент регрессии, угол наклона линии регрессии, характеризующий отношение D Y ¤ D X ,ŷ - теоретическое значение объясняемой переменной) рассчитаем ŷ.
Таблица 2 Сравнение фактических и расчетных значений расходов на потребление товара А при прямолинейной зависимости
| № группы |
Расходы на потребление товара А | Отклонение фактических расходов от расчетных (у - ŷ ) | ||
| фактические (у) |
Расчетные (ŷ) | абсолютные | относительные (в процентах) | |
| 1 | 114,00 | 118,00 | - 4,00 | -4% |
| 2 | 123,00 | 126,00 | - 3,00 | -2% |
| 3 | 132,00 | 133,00 | - 1,00 | -1% |
| 4 | 143,00 | 141,00 | 2,00 | 1% |
| 5 | 152,00 | 148,00 | 4,00 | 3% |
| 6 | 161,00 | 156,00 | 5,00 | 3% |
| 7 | 169,00 | 164,00 | 5,00 | 3% |
| 8 | 171,00 | 171,00 | - | 0% |
| 9 | 178,00 | 179,00 | - 1,00 | -1% |
| 10 | 182,00 | 186,00 | - 4,00 | -2% |
| 11 | 191,00 | 194,00 | - 3,00 | -2% |
| всего | - | - | 0 | - |
Расчет коэффициентов корреляции и детерминации, проверка правильности выбранных факторов и формы связи
Мы выяснили возможность установления корреляционной связи между значениями х и соответствующими значениями у. Теперь необходимо выяснить, как изменение факторного признака влияет на изменение результативного признака.
Вычислим коэффициента корреляции по формуле (3) для расчета линейного коэффициента корреляции:

получим: (3)
![]()
Линейный коэффициент корреляции может принимать любые значения в пределах от минус 1 до плюс 1. Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее связь между признаками. Знак при линейном коэффициенте корреляции указывает на направление связи - прямой зависимости соответствует знак плюс, а обратной зависимости - знак минус.
В нашем примере r = 0,990.
Кроме того, можно рассчитать коэффициент детерминации d , который равен квадрату коэффициента корреляции.
В нашем примере d = 0,981.
Это значит, что изменение расходов на товар А можно на 98,1% объяснить изменением дохода.
Остальные 1,9% могут явиться следствием:
недостаточно хорошо подобранной формы связи;
влияния на зависимую переменную каких-либо других неучтенных факторов.
Целесообразно проверить, не улучшится ли результат, если принять криволинейную форму связи.
Воспользуемся степенной функцией вида: ŷ = axb
Логарифмируем:
lg ŷ = lga + b lgx. (4)
![]() 24,07 = 11*a + 28,85*b, => а=
24,07 = 11*a + 28,85*b, => а= ![]()