Контрольная работа: Расчет коэффициента эластичности и показателей корреляции и детерминации
Fтабл. = 4,46
Fтабл. < Fфакт ; Этот результат можно объяснить сравнительно невысокой теснотой выявленной зависимости и небольшим числом наблюдений.
Задача 13
По заводам, выпускающим продукцию А, изучается зависимость потребления электроэнергии У (тыс. кВт. Ч) от производства продукции - Х1 (тыс.ед.) и уровня механизации труда – Х2 (%). Данные приведены в табл.4.2.
Задание
1. Постройте уравнение множественной регрессии в стандартизованном и натуральном масштабах.
2. Определите показатели частной и множественной корреляции.
3.Найдите частные коэффициенты эластичности и сравните их с Бэтта коэффициентами.
4. Рассчитайте общие и частные F – критерии Фишера.
| Признак | Среднее значение | Среднее квадратическое отклонение | Парный коэффициент корреляции | |
| Y | 1050 | 28 | ryx1 | 0.78 |
| X1 | 425 | 44 | ryx2 | 0.44 |
| X2 | 42.0 | 19 | rx1x2 | 0.39 |
Решение:
1. Постройте уравнение множественной регрессии в стандартизованном и натуральном масштабах.
Линейное уравнение множественной регрессии у от х1 и х2 имеет вид:
![]() .
.
Для расчета его параметров применим метод стандартизации переменных, построим искомое уравнение в стандартизованном масштабе:
![]()
Расчет - коэффициентов выполним по формулам:
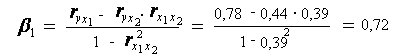
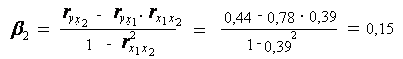
Т.е. уравнение будет выглядеть следующим образом:
![]() .
.
Для построения уравнения в естественной форме рассчитаем b 1 и b 2 ,используя формулы для перехода от к b .
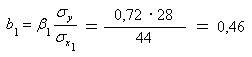
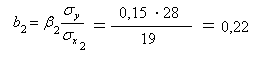
Значение a определим из соотношения:
![]()
![]()
2. Определите показатели частной и множественной корреляции.
Линейные коэффициенты частной корреляции здесь рассчитываются по рекуррентной формуле:
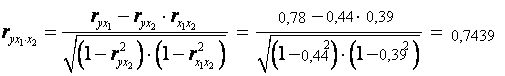
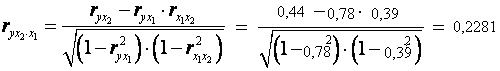
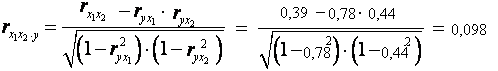
Если сравнить значения коэффициентов парной и частной корреляции, то приходим к выводу, что из-за слабой межфакторной связи (rx 1 x 2 =0,39) коэффициенты парной и частной корреляции отличаются значительно.