Контрольная работа: Расчет коэффициента эластичности и показателей корреляции и детерминации

Зависимость у от х₁ и х₂ характеризуется как тесная, в которой 63 % вариации потребления электроэнергии определяется вариацией учетных в модели факторов: производства продукции и уровня механизации труда. Прочие факторы, не включенные в модель, составляют соответственно 37 % от общей вариации y .

3.Найдите частные коэффициенты эластичности и сравните их с Бэтта коэффициентами.

Для характеристики относительной силы влияния х₁ и х₂ на y рассчитаем средние коэффициенты эластичности:

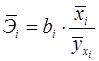
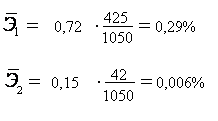
С увеличением производства продукции на 1 % от его среднего потребления электроэнергии возрастает на 0,29 % от своего среднего уровня; при повышении среднего уровня механизации труда на 1 % среднее потребления электроэнергии увеличивается на 0,006% от своего среднего уровня. Очевидно, что сила влияния производства продукции на среднее потребление электроэнергии оказалась больше, чем сила влияния среднего уровня механизации труда.

4. Рассчитайте общие и частные F – критерии Фишера.

Общий F -критерий проверяет гипотезу H ₀ о статистической значимости уравнения регрессии и показателя тесноты связи (R² = 0):

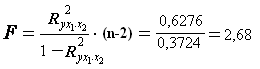
F _табл. = 9,55

Сравнивая F _табл. и F _факт. , приходим к выводу о необходимости не отклонять гипотезу H ₀ и признается статистическая незначимость, ненадежность уравнения регрессии.

Частные F -критерий – F _х1. и F _х2 оценивают статистическую значимость присутствия факторов х ₁ и х ₂ в уравнении множественной регрессии, оценивают целесообразность включения в уравнение одного фактора после другого фактора, т.е. F _х1 оценивает целесообразность включения в уравнение фактора х ₁ после того, как в него был включен фактор х ₂ . Соответственно F _х2 указывает на целесообразность включения в модель фактора х ₂ после фактора х _1.

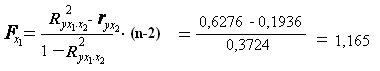
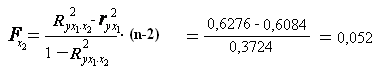
Низкое значение F _х2 (меньше 1) свидетельствует о статистической незначимости прироста r ² _{yx 1} за счет включения в модель фактора х ₂ после фактора х _{1. следовательно,} подтверждается нулевая гипотеза H ₀ о нецелесообразности включения в модель фактора х _2.

Задача 21

Модель денежного и товарного рынков:

R_t = a₁ + b₁₂ Y_t + b₁₄ M_t + e₁ , (функция денежного рынка);

Y_t = a₂ + b₂₁ R_t + b₂₃ I_t + b₂₅ G_t + e₂ ( функция товарного рынка);

I_t = a₃ + b₃₁ R_t + e₃ (функция инвестиций),

где R- процентные ставки;

Y- реальный ВВП;

M- денежная масса;

I- внутренние инвестиции;

G- реальные государственные расходы.

Решение:

R_t = a₁ + b₁₂ Y_t + b₁₄ M_t + e₁ ,

Y_t = a₂ + b₂₁ R_t + b₂₃ I_t + b₂₅ G_t + e₂

I_t = a₃ + b₃₁ R_t + e₃

С_t = Y_t + I_t + G_t