Контрольная работа: Расчет коэффициента эластичности и показателей корреляции и детерминации

Третье уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид

		Rt
I уравнение	0	0	–1	b12	b14	0
II уравнение	0	b23		–1	0	b25
Тождество	-1	1	0	1	0	1

Ранг данной матрицы равен трем, так как определитель квадратной подматрицы не равен нулю:

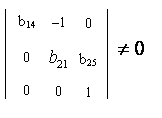
Достаточное условие идентификации для данного уравнения выполняется.

Таким образом, все уравнения модели сверхидентифицируемы. Приведенная форма модели в общем виде будет выглядеть следующим образом:

R_t = a₁ + b₁₁ Y_t + b₁₃ M_t + b₁₅ G_t + b₁₆ G_t + u₁

Y_t = a₂ + b₂₁ R_t + b₂₃ I_t + b₂₅ G_t + b₂₆ G_t + u ₂

I_t = a₃ + b₃₁ R_t + b₃₃ I_t + b₃₅ G_t + b₃₆ G_t + u ₃

С_t = a₄ + b₄₁ R_t + b₄₃ I_t + b₄₅ G_t + b₄₆ G_t + u ₄

Задача 26

Имеются данные об урожайности культур в хозяйствах области:

Варианты	Показатели	Год
		1	2	3	4	5	6	7	8
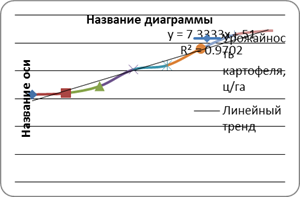
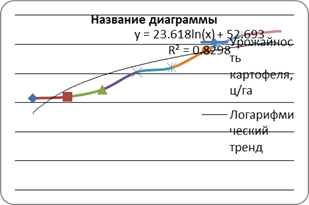
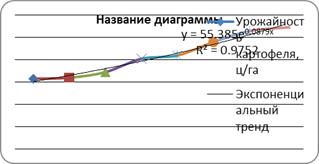
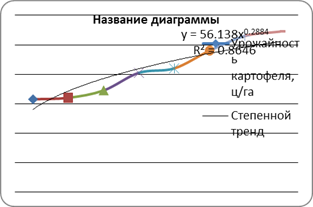
4	Урожайность картофеля, ц/га	63	64	69	81	84	96	106	109

Задание:

1. Обоснуйте выбор типа уравнения тренда.

2. Рассчитайте параметры уравнения тренда.

3.Дайте прогноз урожайности культур на следующий год.

Решение:

1. Обоснуйте выбор типа уравнения тренда.

Построение аналитической функции для моделирования тенденции (тренда) временного ряда называют аналитическим выравнивание временного ряда . Для этого применяют следующие функции:

- линейная

- гипербола

- экспонента

- степенная функция

- парабола второго и более высоких порядков

Параметры трендов определяются обычными МНК, в качестве независимой переменной выступает время t=1,2,…,n, а в качестве зависимой переменной – фактические уровни временного ряда y_t . Критерием отбора наилучшей формы тренда является наибольшее значение скорректированного коэффициента детерминации .