Контрольная работа: Расчет линейной ARC цепей
Нули 
и полюсы 
фильтра определим из уравнений
M(p0 )=1.013∙10-1 4 p0 =0
N(p* )=1.299∙10- 21 p* 2 +2.099∙10-1 6 p* +1.277 ∙10- 10 =0
Получаем, что фильтр имеет один нуль и два комплексно-сопряженных полюса: 
=0 рад/с; 
=-80792±ј∙302950рад/с.
Графическое изображение расположения нулей и полюсов функции на плоскости операторной переменной р=α+jwназывается диаграммой или картой нулей и полюсов
Полюсно–нулевая карта, построенная по этим данным, представлена на рис.4.
3. Расчет частотных характеристик фильтра
Уравнение комплексной передаточной функции 
может быть получено из уравнения операторной передаточной функции 
при замене операторной переменной 
на мнимую частоту 
:
=
.
В свою очередь, после выделения действительных 
, 
и мнимых 
, 
составляющих числителя 
и знаменателя 
дробного выражения комплексной передаточной функции
=
=
,
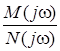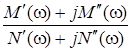легко находятся уравнения АЧХ и ФЧХ цепи:
=
=
;
=
=
-
;
=
при 
;
=
при 
, 
;
=
при , 
;
=
при 
;
=
при 
, 
;
=
при , 
.
Уравнения АЧХ и ФЧХ фильтра получим из дробно-рационального выражения его операторной функции передачи:
=
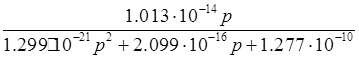
Положив =, получим выражение для комплексной передаточной функции:
==
=
=
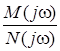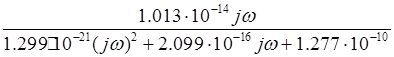Определив модуль этого комплексного выражения, найдем уравнение АЧХ фильтра:
=
==
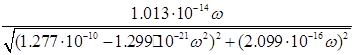
Для нахождения уравнения ФЧХ нужно найти аргумент функции :
=
=
=-.