Контрольная работа: Расчет линейной ARC цепей
![]() =
=![]()
при любой частоте не меняет свой знак. Поэтому ![]() =0 при любой
=0 при любой![]() (
(![]() ≥0).
≥0).
У полинома знаменателя
![]() =
= ![]()
действительная часть
![]() =
=![]()
при частоте ω>313538 рад\с меняет знак. В зависимости от знака действительной части аргумент комплексной функции будет определяться по разным формулам:
![]() =
=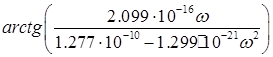
при 0≤![]() <313538 рад/с (
<313538 рад/с (![]() >0);
>0);
![]() =
= 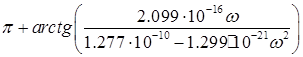
при ![]() ≥313538 рад/с (
≥313538 рад/с (![]() <0).
<0).
![]() =
=![]()
при ![]() =313538 рад/с
=313538 рад/с
Таким образом, уравнение ФЧХ будет выглядеть следующим образом
![]() =-
=-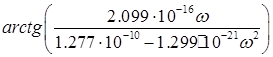
при 0≤![]() <313538рад/с
<313538рад/с
![]() =
=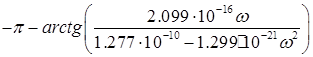
при ![]() >313538рад/с
>313538рад/с
![]() =
=![]()
при ![]() =313538 рад/с
=313538 рад/с
По полученным уравнениям (задавая с определенным шагом значения ![]() и вычисляя соответствующие значения
и вычисляя соответствующие значения ![]() =2π
=2π![]() ) можно построить графики АЧХ
) можно построить графики АЧХ ![]() и ФЧХ
и ФЧХ ![]() фильтра, а также диаграмму АФХ. Для построения амплитудно–фазовой характеристики (АФХ или частотного годографа) целесообразно воспользоваться не показательной формой комплексного параметра KU (jf)=K(ω)ехр(jφ(f)),а алгебраической КU (jf)=A(f)+jB(f)=K(f)cosφ(f) + jK(f)sinφ(f).
фильтра, а также диаграмму АФХ. Для построения амплитудно–фазовой характеристики (АФХ или частотного годографа) целесообразно воспользоваться не показательной формой комплексного параметра KU (jf)=K(ω)ехр(jφ(f)),а алгебраической КU (jf)=A(f)+jB(f)=K(f)cosφ(f) + jK(f)sinφ(f).
По графику определим частоту среза ![]() полосу пропускания
полосу пропускания ![]() , крутизну спада амплитудно-частотной характеристики
, крутизну спада амплитудно-частотной характеристики ![]() :
:
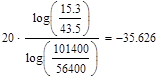
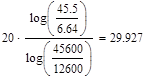
![]() Дб/дек
Дб/дек ![]() Дб/дек
Дб/дек
![]() н =39300 Гц
н =39300 Гц
![]() н =63300Гц
н =63300Гц
![]() →63300-39300=24000Гц
→63300-39300=24000Гц
Расчет частотных характеристик всегда проводятв определенном диапазоне частот, вкотором проявляются основные частотные свойства электрической цепи. Величину диапазона частот можно определить по полюсно-нулевой карте операторной функции.
В качестве нижней граничной частоты fн можно принять значение, близкое к величине