Контрольная работа: Расчет переходных процессов в линейных электрических цепях
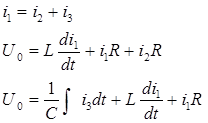
Решая данную систему дифференциальных уравнений, можно получить закон изменения токов и напряжений во времени в момент переходного процесса, не используя специальных методов. Доя упрощения решения системы воспользуемся классическим методом.
1. Токи и напряжения до коммутации.
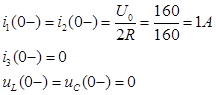
2. Принужденные значения токов и напряжений
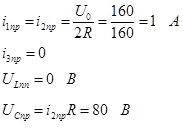
3. Полные значения токов и напряжений в первый момент после коммутации: ![]()
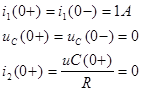
![]()
3. Свободные значения токов и напряжений в первый момент после коммутации:
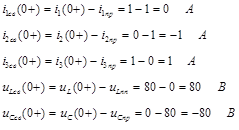
Определим производные свободных токов и напряжений в момент времени непосредственно после коммутации, для чего составим систему уравнений, используя законы Кирхгофа.
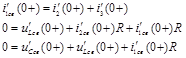
Производные от тока на индуктивности и напряжения на емкости:
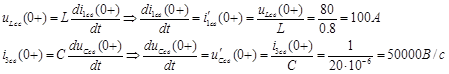
Отсюда
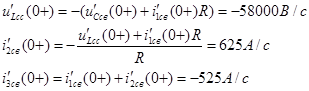
Все полученные результаты занесем в таблицу:
| i1 | i2 | i3 | UL | uс | |
| t= 0 + | 1 | 0 | 1 | 80 | 0 |
| t=∞ | 1 | 1 | 0 | 0 | 80 |
| Iс в (0+) | 0 | -1 | 1 | ||
| Uс в (0+) | 80 | -80 | |||
| I’с в (0+) | 100 | 625 | |||
| U’с в (0+) | -58000 | 50000 |
Составим характеристическое уравнение (для послекоммутационного режима) и определим его корни:
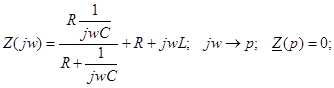
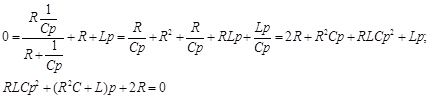
Подставим численные значения параметров цепи:
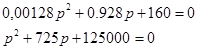
Решив квадратное уравнение получаем:
р1 = - 282.461
р2 = - 442.539
7. Определим постоянные интегрирования А1 и А2 , и запишем выражения для токов и напряжений а) Для тока i1св :