Контрольная работа: Расчет вероятностей событий
Середины интервалов 
Средняя арифметическая 
где 
- варианты дискретного ряда или середины интервалов вариационного ряда, 
- соответствующие им частоты.
Дисперсия 
.
Среднее квадратическое отклонение 
.
| № | Значения | № группы | Интервалы | Частота | |
| 1 | 1 | нач | кон | ||
| 2 | 2 | 1 | 1,0 | 5,5 | 3 |
| 3 | 5 | 2 | 5,5 | 10,0 | 5 |
| 4 | 7 | 3 | 10,0 | 14,5 | 15 |
| 5 | 9 | 4 | 14,5 | 19,0 | 17 |
| 6 | 10 | 5 | 19,0 | 23,5 | 2 |
| 7 | 10 | 6 | 23,5 | 28,0 | 3 |
| 8 | 10 | ||||
| 9 | 11 | ||||
| 10 | 11 | ||||
| 11 | 11 | ||||
| 12 | 12 | ||||
| 13 | 12 | ||||
| 14 | 13 | ||||
| 15 | 13 | ||||
| 16 | 14 | ||||
| 17 | 14 | ||||
| 18 | 14 | ||||
| 19 | 14 | ||||
| 20 | 14 | ||||
| 21 | 14 | ||||
| 22 | 14 | ||||
| 23 | 14 | ||||
| 24 | 15 | ||||
| 25 | 15 | ||||
| 26 | 15 | ||||
| 27 | 15 | ||||
| 28 | 15 | ||||
| 29 | 15 | ||||
| 30 | 15 | ||||
| 31 | 16 | ||||
| 32 | 16 | ||||
| 33 | 16 | ||||
| 34 | 17 | ||||
| 35 | 17 | ||||
| 36 | 17 | ||||
| 37 | 18 | ||||
| 38 | 18 | ||||
| 39 | 19 | ||||
| 40 | 19 | ||||
| 41 | 20 | ||||
| 42 | 22 | x min | 1 | ||
| 43 | 24 | x max | 28 | ||
| 44 | 26 | h | 4,5 | ||
| 45 | 28 | ||||
| № группы | Интервалы | Частота | Промежуточные вычисления | |||||
| нач | кон | сер | ni | xcp *ni | (x-Xcp) | (x-Xcp)2 | ni* (x-Xcp)2 | |
| 1 | 1,0 | 5,5 | 3,25 | 3 | 9,75 | -10,9 | 118,81 | 356,43 |
| 2 | 5,5 | 10,0 | 7,75 | 5 | 38,75 | -6,4 | 40,96 | 204,80 |
| 3 | 10,0 | 14,5 | 12,25 | 15 | 183,75 | -1,9 | 3,61 | 54,15 |
| 4 | 14,5 | 19,0 | 16,75 | 17 | 284,75 | 2,6 | 6,76 | 114,92 |
| 5 | 19,0 | 23,5 | 21,25 | 2 | 42,50 | 7,1 | 50,41 | 100,82 |
| 6 | 23,5 | 28,0 | 25,75 | 3 | 77,25 | 11,6 | 134,56 | 403,68 |
| | 45 | 636,75 | | 1234,80 | ||||
 | 14,15 | S2 | 27,44 | |||||
| | 5,24 | |||||||
Среднее значение 
Дисперсия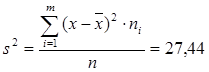 
Среднее квадратическое отклонение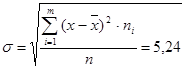 
Ответ :
, 
, 
Задание № 5
Некоторая случайная величина подчиняется закону нормального распределения с математическим ожиданием 50 и дисперсией 36. Найти вероятность того, что отдельное значение случайной величины заключено в интервале от 40 до 60.
Решение:
Пусть X – случайная величина подчиняется закону нормального распределения
По условию 
и 
Найти : 
Для нормального распределения СВ X
где Ф(Х) – функция Лапласа, дифференциальная функция нормального закона имеет вид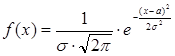 
.
Значения Ф(Х) – табулированы
Ответ : 
Задание №6
Определить вероятность того, что истинное значение расстояния отличается от среднего (1000 м), полученного в 100 опытах, не более, чем на 5 м, если стандартное отклонение 25 м.
Решение:
Пусть X – случайная величина расстояния, м
По условию 
Найти : 
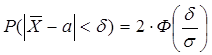
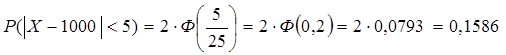
Ответ : 