Контрольная работа: Решение задач по курсу теории вероятности и математической статистики

№ 42

Определить вероятность того, что нормально распределённая величина Х примет значение, принадлежащее интервалу (α;β) если известны математическое ожидание а и среднее квадратическое отклонение σ. Данные: α = 5; β = 14; а = 9; σ = 5.

Используя формулу имеем

Поскольку функция Лапласа есть нечетная, можем записать:

№ 52

По данному статистическому распределению выборки

хі	7,6	8	8,4	8,8	9,2	9,6	10	10,4
mі	6	8	16	50	30	15	7	5

Определить: а) выборочную среднюю; б) выборочную дисперсию;в) выборочное среднее квадратическое отклонение.

Для решения задачи введём условную переменную

где С – одно из значений х_і , как правило, соответствующее наибольшему значению m_і , а h – это шаг (у нас h = 0,4).

Пусть С = 8,8. Тогда

Заполним таблицу:

xi	mi	xi ´	xi mi	(xi ´)²mi
7,6	6	– 3	– 18	54
8	8	– 2	– 16	32
8,4	16	– 1	– 16	16
8,8	50	0	0	0
9,2	30	1	30	30
9,6	15	2	30	60
10	7	3	21	63
10,4	5	4	20	80
∑ = 137	∑ = 51	∑ = 335

Используя таблицу, найдём

;

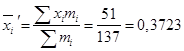D(x´) = ∑(x_i ´)²m_i – (x_i ´)² = – 0,3723² = 2,3067.

Теперь перейдем к фактическим значениям х и D(x):

x = x´h + C = 0,3723∙0,4 + 8,8 = 8,9489; D(x) = D(x´)∙h² = 2,3067∙0,4² = 0,3961;

σ(x) = √D(x) = √0,3961 = 0,6075.

№ 62

По данной корреляционной таблице

у х	4	8	12	16	20	24	ny
10	2	5	7
20	6	8	4	18
30	8	46	10	64
40	5	20	4	29
50	3	14	2	5	22
nx	2	19	62	48	6	3	n = 140

найти выборочное уравнение регрессии.

Для упрощения расчетов введём условные переменные

Составим таблицу.

vu	– 2	– 1	0	1	2	3	nv	nuv uv
– 2	2 4	5 2	7	18
– 1	6 1	8 0	4 –1	18	2
0	8 0	46 0	10 0	64	0
1	5 0	20 1	4 2	29	28
2	3 0	14 2	2 4	5 6	22	66
nu	2	19	62	48	6	3	n = 140	∑ = 114

Последовательно получаем:

;

;

;

;

σ_u ² = – (u)² = 0,9 – 0,329² = 0,792; σ_u = √0,792 = 0,89;