Контрольная работа: Система координат

Точки пересечения линии главного меридиана с поверхностью сферы обозначим, как М1 и М2

Далее мы поступаем следующим образом:

Через центр сферы точку О в плоскости главного меридиана проведем прямую, перпендикулярную линии главного меридиана. Эта прямая носит название ПОЛЯРНАЯ ОСЬ .

Полярная ось пересечет поверхность сферы в двух точках, которые называются ПОЛЮСАМИ СФЕРЫ. Обозначим эти точки, как Р1 и Р2.

Определение координат точки в пространстве

Теперь рассмотрим процесс определения координат точки в пространстве, а так же дадим наименования этим координатам. Для полноты картины, при определении положения точки, укажем основные направления, от которых производится отсчет координат, а так же положительное направление при отсчете.

1. Задаем положение в пространстве точки отсчета (или точки наблюдения). Обозначим эту точку буквой О.

2. Строим сферу, радиус которой равен длине радиус-вектора точки А. (Радиус-вектор точки А – это расстояние между точками О и А). Центр сферы располагается в точке отсчета О.

3. Задаем положение в пространстве плоскости ЭКВАТОРА, а соответственно плоскости ГЛАВНОГО МЕРИДИАНА. Следует напомнить, что эти плоскости взаимно перпендикулярны и являются центральными.

4. Пересечение этих плоскостей с поверхностью сферы определяет нам положение круга экватора, круга главного меридиана, а так же направление линии главного меридиана и полярной оси.

5. Определяем положение полюсов полярной оси и полюсов линии главного меридиана. (Полюса полярной оси – точки пересечение полярной оси с поверхностью сферы. Полюса линии главного меридиана – это точки пересечения линии главного меридиана с поверхностью сферы).

6. Через точку А и полярную ось строим плоскость, которую назовем плоскостью меридиана точки А. При пересечении этой плоскости с поверхностью сферы получится большой круг, который мы назовем МЕРИДИАНОМ точки А.

7. Меридиан точки А пересечет круг ЭКВАТОРА в некоторой точке, которую мы обозначим, как Е1

8. Положение точки Е1 на экваториальном круге определяется длиной дуги, заключенной между точками М1 и Е1. Отсчет ведется ПРОТИВ часовой стрелки. Дуга экваториального круга, заключенная между точками М1 и Е1 называется ДОЛГОТОЙ точки А. Долгота обозначается буквой  .

Подведем промежуточный итог. На данный момент нам известны ДВЕ из ТРЕХ координат, описывающих положение точки А в пространстве – это радиус-вектор (r) и долгота (). Теперь мы будем определять третью координату. Эта координата определяется положением точки А на ее меридиане. Но вот положение начальной точки, от которой происходит отсчет, однозначно не определено: мы можем начинать отсчет как от полюса сферы (точка Р1), так и от точки Е1, то есть от точки пересечения линий меридиана точки А и экватора (или другими словами – от линии экватора).

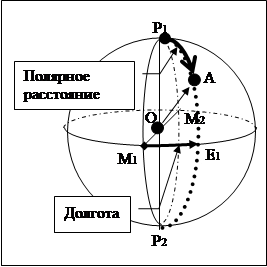
В первом случае, положение точки А на меридиане называется ПОЛЯРНЫМ РАССТОЯНИЕМ (обозначается как р ) и определяется длиной дуги, заключенной между точкой Р1 (или точкой полюса сферы) и точкой А. Отсчет ведется вдоль линии меридиана от точки Р1 к точке А.

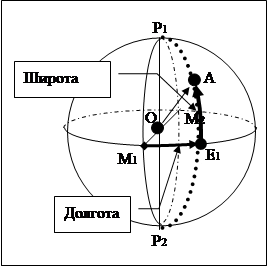
Во втором случае, когда отсчет ведется от линии экватора, положение точки А на линии меридиана называется ШИРОТОЙ (обозначается как   и определяется длиной дуги, заключенной между точкой Е1 и точкой А.

Теперь мы можем окончательно сказать, что положение точки А в сферической системе координат определяется через:

· длину радиуса сферы ( r ),

· длину дуги долготы (  ),