Контрольная работа: Система координат

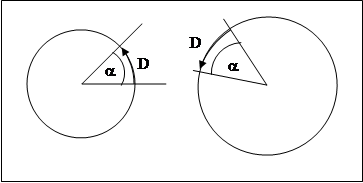
1. В одной и той же окружности длины дуг можно измерять угловой мерой.

2. Относительные длины дуг, принадлежащих различным окружностям, будут равны, если равны центральные углы, опирающиеся на эти дуги.

У Вас, мой дорогой читатель, возникает закономерный вопрос – к чему это столь длинное и нудное объяснение? Но вспомним определение, данное нами Небесной сфере. Из этого определения явствует, что все небесные тела располагаются на поверхности Небесной сферы, то есть, так получается, что радиус-векторы всех небесных объектов – ОДИНАКОВЫ. А отсюда следует, что положение небесных объектов на Небесной сфере можно ОДНОЗНАЧНО определить не тремя, а ДВУМЯ координатами – это, в общем случае:

· долгота ( ) и широта ( ). [ A (  ) ] или

· долгота ( ) и полярное расстояние ( ). [ A (  ) ]

причем, эти координаты измеряются центральными углами между соответствующими направлениями и измеряются угловой мерой.

Величина долготы ( ) соответствует величине центрального угла между ЛИНИЕЙ ГЛАВНОГО МЕРИДИАНА и ЛИНИЕЙ МЕРИДИАНА точки А

Величина полярного расстояния ( ) соответствует величине центрального угла между ПОЛЯРНОЙ ОСЬЮ и НАПРАВЛЕНИЕМ на точку А