Контрольная работа: Система координат

В этом случае координаты точки А запишутся следующим образом: А(r, , p)

Если пользоваться иной системой отсчета, то положение точки А в сферической системе координат определяется через:

· длину радиуса сферы ( r ),

· длину дуги долготы (  ),

· длину дуги широты (  )

В этом случае координаты точки А запишутся следующим образом: А(r, , )

Способы измерения дуг

Возникает вопрос – как же нам измерить эти дуги? Самый простой и естественный способ – это провести непосредственное измерение длин дуг гибкой линейкой, и это возможно, если размеры сферы сравнимы с размерами человека. Но как поступить, если это условие не выполнимо?

В этом случае мы прибегнем к измерению ОТНОСИТЕЛЬНОЙ длины дуги. За эталон же мы примем длину окружности, частью которой является интересующая нас дуга. Как это можно сделать?

Нам известно, что длина окружности пропорциональна ее радиусу. Аналитически это утверждение запишется как:

Естественно, что длина дуги так же будет пропорциональна радиусу окружности:

Рассмотрим соотношение:

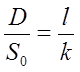
Как мы видим, это соотношение уже НЕ ЗАВИСИТ от радиуса окружности.

Теперь вспомним ОПРЕДЕЛЕНИЕ окружности. Окружность – это геометрическое место точек плоскости, равноудаленных от одной ее точки (центра). Отрезок прямой, соединяющей центр окружности с одной из ее точек называется РАДИУСОМ окружности.

Из определения, данное для окружности, получается, что ВСЕ радиусы одной и той же окружности РАВНЫ между собой.

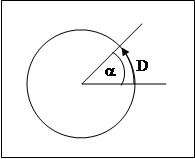
Если мы проведем ДВА радиуса, то у нас получится угол, который носит название ЦЕНТРАЛЬНОГО угла. Как мы видим, центральный угол опирается на дугу окружности. Очевидно, что длина дуги, описываемой концом радиуса, пропорциональна величине соответствующего центрального угла.

Если радиус опишет один оборот, то длина дуги будет равна длине окружности.

Рассмотрим еще раз соотношение 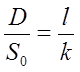, которое говорит, что в одной и той же окружности относительная длина дуги не зависит от радиуса окружности. Подставим вновь полученные выражения для длины дуги и длины окружности:

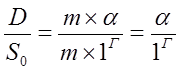
Таким образом, у нас получается, что относительная длина дуги численно равна величине центрального угла, опирающемуся на эту дугу.