Контрольная работа: Статистическое изучение взаимосвязей

20

0,32

0,36

+

-

в

Итого

5,44

16,58

Получаем:

= 4, = 16,

Тогда

,

что свидетельствует от наличии

обратной зависимости.

При малом объеме исходной информации коэффициент Фехнера отвечает также на вопрос о наличии связи.

Более современным показателем степени тесноты связи является линейный коэффициент корреляции r .

При расчете этого показателя учитывается не только знаки отклонений индивидуальных значений от средней, но и сами величины таких отклонений, т.е. . Однако непосредственно сопоставить полученные абсолютные величины нельзя, т.к они обычно выражаются в разных единицах. Поэтому сравнению могут подлежать отклонения выраженные в относительных величинах, обычно в долях среднего квадратичного отклонения (нормируемые отклонения).

Так для факторного признака эта величина будет равна 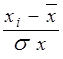, а для результативного ;

Для того, чтобы на основе сопоставления рассчитанных нормируемых отклонений получить обобщающую характеристику степени тесноты связи между признаками рассчитывают среднее произведение нормированных отклонений. Полученная таким образом средняя и является линейным коэффициентом корреляции r

;

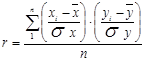преобразовав формулу:

;

Далее

.

Линейный коэффициент принимает значения от - 1 до +1.

Чем ближе коэффициент r по абсолютной величине к 1, тем теснее корреляционная связь. Положительный знак r указывает на прямо пропорциональную зависимость, а отрицательный на обратно. пропорциональную зависимость.

Для примера рассчитаем r