Контрольная работа: Теория игр и статических решений

Решение:

Заменим знаки вопроса на неизвестные переменные следующим образом:

a	b
A	7 y	x 4
B	t 25	9 z

Попытаемся заполнить пропуски в таблице так, чтобы равновесия по Нэшу достигались в вариантах игры (A, a), (B, a), (B, b), а при игре (A, b) равновесие по Нэшу не достигалось. Тогда должна выполняться система неравенств (объедим их парами для каждого варианта игры):

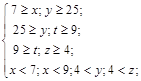Откуда получаем:

Возьмем минимальные целые числа, удовлетворяющие системе неравенств. Получим игру:

a	b
A	7 25	6 4
B	9 25	9 5

Действительно, в данной игре варианты (A, a), (B, a), (B, b) будут являться равновесиями по Нешу, т.к. здесь ни одному из игроков не выгодно изменить свою стратегию, а при игре (A, b) каждому из игроков выгодно изменить свою стратегию.

Найдем равновесие в смешанных стратегиях. Предположим, что первый игрок с вероятностью µ играет стратегию A, соответственно с вероятностью (1 - µ) – стратегию B. Второй игрок с вероятностью ν играет стратегию a, а с вероятностью (1 - ν) - стратегию b. Тогда функции выигрыша игроков будут выглядеть следующим образом:

;

Тогда функции отклика будут следующими:

Имеем 2 равновесия в смешанных стратегиях. Если второй игрок играет стратегию b, то первый игрок всегда будет играть стратегию B. Если первый игрок играет стратегию А, то второй игрок будет играть стратегию a.

Решением же в доминируемых стратегиях будет (B, a).