Контрольная работа: Теория игр и статических решений
d) Составьте платежную матрицу этой игры. Найдите равновесия в чистых стратегиях.
e) Нарисуйте линии откликов игроков и найдите смешанные равновесия в этой игре.
f) Допустим теперь, что у игроков теперь 3 стратегии: «не уступить», «уступить» и «уступить пол-лыжни». Если оба уступили друг другу пол-лыжни, то потери каждого 4 секунд, если же один уступил пол-лыжни, а второй - нет, то лыжники столкнутся, и потери при столкновении у уступившего – 29 секунд, у неуступившего - 4 секунды. Найдите все равновесия по Нэшу (в чистых и в смешанных стратегиях).
Решение:
a) Составим платежную матрицу этой игры:
| У | Н | |
| У |
-9 -9 |
0 -9 |
| Н |
-9 0 |
-25 -25 |
В чистых стратегиях равновесия в данной игре нет.
b) Найдем равновесие в смешанных стратегиях.
Предположим, что первый игрок с вероятностью µ играет стратегию У, соответственно с вероятностью (1 - µ) – стратегию Н. Второй игрок с вероятностью ν играет стратегию У, а с вероятностью (1 - ν) - стратегию Н.
Функции выигрыша игроков:
![]()
![]()
Соответственно функции откликов:
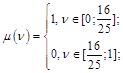
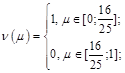
Имеем 2 точки пересечений линий, соответствующие равновесиям в смешанных стратегиях:
2. (Н; У), то есть первый игрок всегда не уступает, а второй – уступает;
3. (У; Н), то есть первый игрок всегда уступает, а второй – не уступает;
4. Каждый из игроков с вероятность 16/25 уступает лыжню и с вероятностью 9/25 не уступает лыжню.
c) Составим платежную матрицу игры:
| У | Н | УП |
| У |
-9 -9 |
0 К-во Просмотров: 474
Бесплатно скачать Контрольная работа: Теория игр и статических решений
|