Контрольная работа: Теория телетрафика

Y – средняя интенсивность нагрузки Y=a*v=0,45*9=4,05

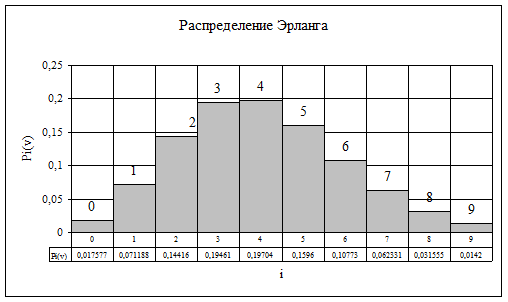
Рисунок 2 Распределение Эрланга

Математическое ожидание и дисперсия числа занятых линий, вероятность занятия которых подчиняется распределению Эрланга, соответственно равны:

в) Распределение Пуассона используется при N, v → ∞ и имеет вид:

где Y – средняя интенсивность нагрузки Y=a*v=0,45*9=4,05

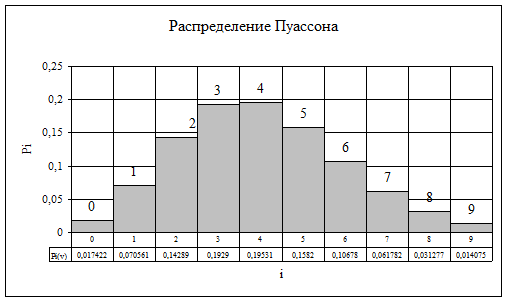
Рисунок 3 Распределение Пуассона

Математическое ожидание и дисперсия числа занятых линий, в бесконечном пучке линий равны между собой и вычисляются по формуле:

Потоки вызовов. Основные свойства и характеристики

Задание 2

На коммутационную систему поступает простейший поток вызовов с интенсивностью Y.

1. Рассчитать вероятности поступления менее k вызовов за промежуток времени [0, t*): P_k (t*), где t*= 0,5; 1,0; 1,5; 2,0.

2. Построить функцию распределения промежутков времени между двумя последовательными моментами поступления вызовов. F(t*), где t*= 0; 0,1; 0,2; ...

3. Рассчитать вероятность поступления не менее k вызовов за интервал времени [0, t*): P_{i ³ k} {t*), где t*= 1.

Примечание:

Для расчета значения Y и v взять из задания 1. Число вызовов k определить из выражения: k = [v/2] - целая часть числа.

Для построения графика, рассчитать не менее пяти значений F(t*). Результаты расчета привести в виде таблицы значений F(t*) и t*.

Расчет членов суммы P_{i ³ k} {t*) провести не менее, чем для восьми членов суммы.

Решение

1. Вероятность поступления менее k вызовов за промежуток времени [0, t*): P_k (t*), где t*= 0,5; 1,0; 1,5; 2,0; вычислим по формуле:

, где k =0, 1, 2,....;

Y=4,5; v=9 – из первого задания; k=v/2=9/2=4,5=5

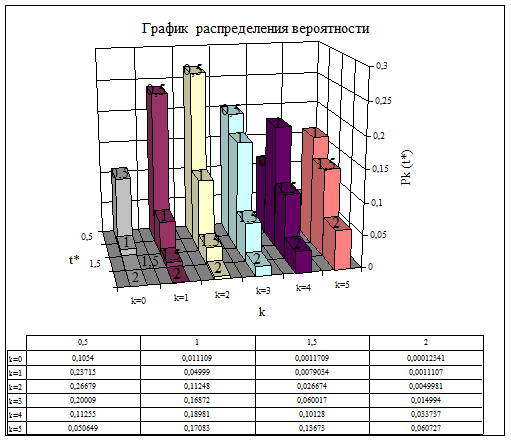
Рисунок 4 График распределения вероятности