Контрольная работа: Вычисление интегралов
Пусть требуется найти объем V тела (рис 5), причем известны площади сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси Ox : S = S ( x ), a ≤ x ≤ b [5]
Применим схему II (метод дифференциала).
|
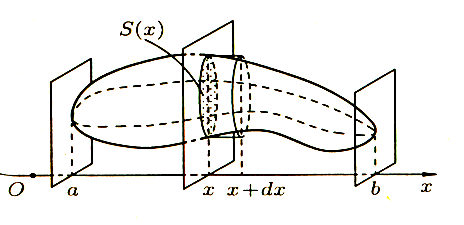
1. Через произвольную точку x![]() [а; b]проведем плоскость П, перпендикулярную оси Ох . Обозначим через S ( x ) площадь сечения тела этой плоскостью; S ( x ) считаем известной и непрерывно изменяющейся при изменении x. Через v ( x ) обозначим объем части тела, лежащее левее плоскости П. Будем считать, что на отрезке [а; x]величина v есть функция от x , т.е. v = у( x ) (v(a) = 0, v(b) = V ).
[а; b]проведем плоскость П, перпендикулярную оси Ох . Обозначим через S ( x ) площадь сечения тела этой плоскостью; S ( x ) считаем известной и непрерывно изменяющейся при изменении x. Через v ( x ) обозначим объем части тела, лежащее левее плоскости П. Будем считать, что на отрезке [а; x]величина v есть функция от x , т.е. v = у( x ) (v(a) = 0, v(b) = V ).
2. Находим дифференциал dV функции v = v(x). Он представляет собой
«элементарный слой» тела, заключенный между параллельными плоскостями, пересекающими ось Ох в точках x и x + Δx, который приближенно может быть принят за цилиндр с основанием S ( x ) и высотой dx . Поэтому дифференциал объема dV = S (х) d х.
3. Находим искомую величину V путем интегрирования d А в пределах от a до b:
V = ![]() S ( x ) dx
S ( x ) dx
Формула объема тела по площади параллельных сечений
Пример:Найти объем эллипсоида ![]() (рис 6) [5]
(рис 6) [5]
|
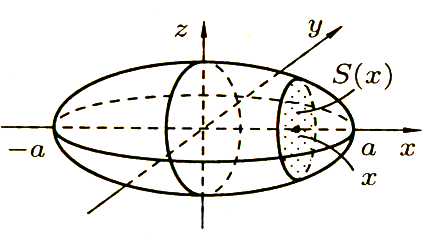
Решение: Рассекая эллипсоид плоскостью, параллельной плоскости OYZ и на расстоянии х от нее (-a ≤ x ≤ b. ), получим эллипс
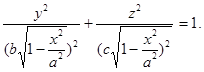
Площадь этого эллипса равна S(x) = ![]() bc (1 –
bc (1 – ![]() ). Поэтому, по формуле имеем
). Поэтому, по формуле имеем
V = ![]() bc
bc![]() (1 –
(1 – ![]() ) dx =
) dx = ![]()
![]() abc .
abc .
Объём тела вращения
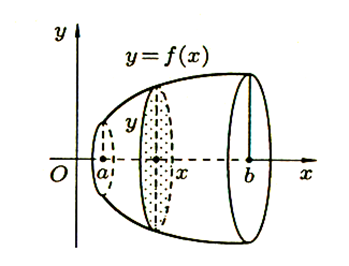
Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная непрерывной линией у = f (х) ≥ 0, отрезком а ≤ х ≤ b и прямыми х = а и х = b (рис 7). Полученная от вращения фигура называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси O х ), есть круг с радиусом у = f (х). Следовательно,S ( x )=![]() y
y![]() .
.
Применяя формулу
V = ![]() S ( x ) dx
S ( x ) dx
объема тела по площадипараллельных сечений, получаем
![]()
V![]() =
= ![]()
![]() y
y![]() dx.
dx.
Если криволинейная трапеция ограничена графиком непрерывной функции x = ![]() (x) ≥ 0 и прямыми x = 0, y = c, y = d (c <
(x) ≥ 0 и прямыми x = 0, y = c, y = d (c <
d), то объем тела, образованного вращением этой трапеции вокруг оси Оу, по аналогии с формулой
V = ![]() S(x) dx ,
S(x) dx ,
равен
V = ![]()
![]() x
x![]() dy .
dy .
Пример:Найти объем тела, образованного вращением фигуры, ограниченной линиями у = ![]() , x = 0, у = 2
, x = 0, у = 2![]() вокруг оси Оу . [5]
вокруг оси Оу . [5]
Решение: По формуле
V = ![]()
![]() x
x![]() dy .
dy .