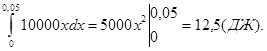Контрольная работа: Вычисление интегралов

V = 2ydy = y = 8.

5. Нахождение площади поверхности тел вращения

Пусть кривая АВ является графиком функции у = f (х) ≥ 0, где х [а; b ], а функция у = f (х) и ее производная у' = f '(х) непрерывны на этом отрезке.

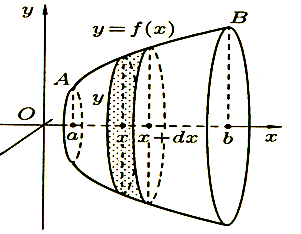
Найдем площадь S поверхности, образованной вращением кривой АВ вокруг оси Ох (рис 8).

Применим схему II (метод дифференциала).

Через произвольную точку х [а; b] проведем плоскость П, перпендикулярную оси Ох. Плоскость П пересекает поверхность вращения по окружности с радиусом у – f (х) . Величина S поверхности части фигуры вращения, лежащей левее плоскости, является функцией от х, т.е. s = s (х) (s(а) = 0 и s(b) = S).

Дадим аргументу х приращение Δх = d х. Через точку х + d х [а; b]также проведем плоскость, перпендикулярную оси Ох. Функция s = s(х) получит приращение Δs, изображенного на рисунке в виде «пояска».

Найдем дифференциал площади ds , заменяя образованную между сечениями фигуру усеченным конусом, образующая которого равна dl , а радиусы оснований равны у и у + d у. Площадь его боковой поверхности равна: = 2 ydl + dydl.

Отбрасывая произведение d у d 1 как бесконечно малую высшего порядка, чем ds , получаем ds = 2 у dl , или, так как d 1 = dx .

Интегрируя полученное равенство в пределах от х = а до х = b,получаем

S= 2y dx .

Если кривая AB задана параметрическими уравнениями x = x(t), y = y(t), t≤ t≤ t, то формула для площади поверхности вращения принимает вид

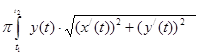S = 2dt .

Пример:Найти площадь поверхности шара радиуса R. [5]

Решение: Можно считать, что поверхность шара образована вращением полуокружности y = , – R ≤ x ≤ R, вокруг оси Ox. По формуле S= 2y dx находим

S=2 =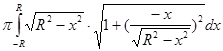

6. Нахождение работы переменной силы

Работа переменной силы

Пусть материальная точка М перемещается вдоль оси Ох под действием переменной силы F = F (х), направленной параллельно этой оси. Работа, произведенная силой при перемещении точки М из положения х = а в положение х = b (а < b Ь), находится по формуле

A =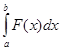

Пример:

Какую работу нужно затратить, чтобы растянуть пружину на 0,05 м, если сила 100 Н растягивает пружину на 0,01 м? [5]

Решение:

По закону Гука упругая сила, растягивающая пружину, пропорциональна этому растяжению х, т.е. F = k х, где k– коэффициент пропорциональности. Согласно условию задачи, сила F = 100 Н растягивает пружину на х = 0,01 м; следовательно, 100 = k 0,01, откуда k = 10000; следовательно, F =10000 х.

Искомая работа на основании формулы

A =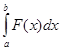

равна

A =