Контрольная работа: Вычисление интегралов

Пример:

Найти работу, которую необходимо затратить, чтобы выкачать через край жидкость из вертикального цилиндрического резервуара высоты Н м и радиусом основания Rм (рис 13). [5]

Решение:

Работа, затрачиваемая на поднятие тела весом р на высоту h, равна р • Н. Но различные слои жидкости в резервуаре находятся на различных глубинах и высота поднятия (до края резервуара) различных слоев не одинакова.

Для решения поставленной задачи применим схему II (метод дифференциала). Введем систему координат.

1) Работа, затрачиваемая на выкачивание из резервуара слоя жидкости толщиной х (0 ≤ х ≤ Н), есть функция от х, т.е. А = А(х), где (0 ≤ х ≤ Н) ( A (0) = 0, A (H) = А₀ ).

2) Находим главную часть приращения ΔA при изменении х на величину Δх = dx, т.е. находим дифференциал dА функции А(х).

Ввиду малости dх считаем, что «элементарный» слой жидкостинаходится на одной глубине х(от края резервуара). Тогда dА = dрх, где dр – вес этого слоя; он равен g АV, где g – ускорение свободного падения, – плотность жидкости, dv – объем «элементарного» слоя жидкости (на рисунке он выделен), т.е. dр = g . Объем указанного слоя жидкости, очевидно, равен , где dx – высота цилиндра (слоя), – площадь его основания, т.е. dv= .

Таким образом, dр = . и

3) Интегрируя полученное равенство в пределах от х = 0 до х = Н, находим

A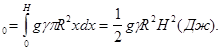

8. Вычисление интегралов с помощью пакета MathCAD

При решении некоторых прикладных задач требуется использовать операцию символического интегрирования. При этом программа MathCad может пригодиться как на начальном этапе (хорошо знать ответ заранее или знать, что он существует), так и на заключительном этапе (хорошо проверить полученный результат с использованием ответа из другого источника или решения другого человека).

При решении большого количества задач можно заметить некоторые особенности решения задач при помощи программы MathCad. Попытаемся понять на нескольких примерах, как работает эта программа, проанализируем решения, полученные с её помощью и сравним эти решения с решениями, полученными другими способами.

Основные проблемы при использовании программы MathCad заключаются в следующем:

а) программа даёт ответ не в виде привычных элементарных функций, а виде специальных функций, известных далеко не всем;

б) в некоторых случаях «отказывается» давать ответ, хотя решение у задачи имеется;

в) иногда невозможно воспользоваться полученным результатом из-за его громоздкости;

г) решает задачу не полностью и не делает анализа решения.

Для того чтобы решить эти проблемы, необходимо использовать сильные и слабые стороны программы.

С её помощью легко и просто вычислять интегралы от дробно-рациональных функций. Поэтому рекомендуется использовать метод замены переменной, т.е. предварительно подготовить интеграл для решения. Для этих целей могут быть использованы подстановки, разобранные выше. Также следует иметь в виду, что полученные результаты необходимо исследовать на совпадение областей определения исходной функции и полученного результата. Кроме этого, некоторые полученные решения требуют дополнительного исследования.

Программа MathCad освобождает обучаемого или исследователя от рутинной работы, но не может освободить его от дополнительного анализа как при постановке задачи, так и при получении каких-либо результатов.

Выводы

В данной работе были рассмотрены основные положения, связанные с изучением приложений определённого интеграла в курсе математики.

– был проведен анализ теоретической основы решения интегралов;

– материал был подвергнут систематизации и обобщению.

В процессе выполнения курсовой работы были рассмотрены примеры практических задач в области физики, геометрии, механики.

Заключение