Контрольная работа: Вычисление наибольшей прибыли предприятия

Содержание

Задача 1. 2

Задача 2. 4

Задача 3. 6

Задача 1

Пусть х (млн. шт.) – объем производства, С(х)=2х³ -7х и D(x)=2х² +9х+15 – соответственно функция издержек и доход некоторой фирмы. При каком значении х фирма получит наибольшую прибыль π(х)? какова эта прибыль?

Решение

Прибыль фирмы является разницей между доходом и издержками фирмы:

,

,

.

Найдем наибольшее значение прибыли путем нахождения максимума функции .

- не удовлетворяет условию задачи,

.

График функции прибыли представлен на рисунке 1.

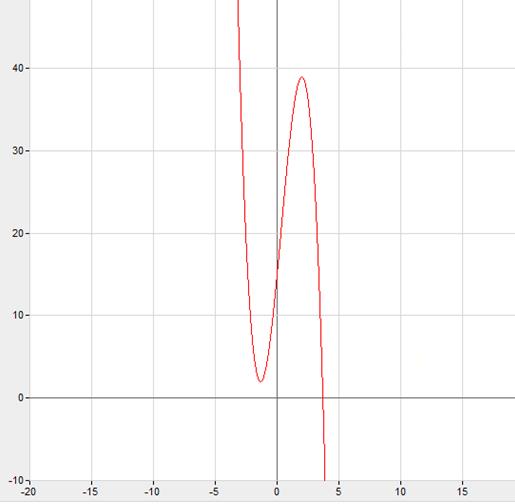
Рисунок 1 - График функции прибыли

Как видно из рисунка 1, функция прибыли в точке х=2 достигает максимального значения. Следовательно, фирма получает наибольшую прибыль при объеме производства 2 млн. шт. и эта прибыль составляет:

млн. у.е.

Ответ: наибольшую прибыль фирма получит при объеме производства 2 млн. шт. и эта прибыль составит 39 млн. у.е.

Задача 2

Заданы: функция прибыли , где х₁ и х₂ – объемы некоторых ресурсов; цены р₁ =1 и р₂ =1 за единицу каждого ресурса соответственно (в некоторых у.е.); бюджетное ограничение I=150 на затраты по приобретению указанных ресурсов (в тех же у.е.). При каких значениях объемов используемых ресурсов фирма–производитель получит наибольшую прибыль?

Решение

Задача сводится к поиску максимума функции при существовании ограничения :

при .

,

--> ЧИТАТЬ ПОЛНОСТЬЮ <--