Контрольная работа: Задачі максимізації та оптимізації діяльності підприємства

1. Найпростіша задача на максимізацію прибутку компанії

Компанія робить два продукти в кількості x1 і x2 тонн за місяць відповідно. Тонна першого продукту приносить 12 тис. грн.. прибутку, а тонна другого – 8 тис. грн. Виробничі потужності компанії дозволяють випускати не більше 100 тонн двох продуктів разом, при цьому виробництво першого продукту не може перевищувати більше ніж у три рази виробництво другого. Треба визначити оптимальний обсяг виробництва, що приносить компанії оптимальний прибуток.

Стосовно до даної задачі цільова функція (критерій оптимальності) має вид

F(x1, x2,……xn)=F(x1,x2)=12x1+8x2 тис. грн.

Обсяги випуску x1 і x2 є свідомо позитивні величини, тобто

x1 ≥ 0; x2 ≥ 0.

Між значеннями x1 і x2 маються зв'язки

x1 + x2 ≤ 100 x1 ≤ 3 x2

Таким чином, підходимо до типової задачі лінійного математичного програмування, коли треба відшукати значення керуючих параметрів x1, x2, що додають максимальне значення цільової функції 12x1 + 8x2 з урахуванням фіксованих зв'язків і обмежень.

Постановку і розв’язання цієї задачі зручно проілюструвати графічно, відобразивши зв'язки й обмеження в системі координат x1, x2, як зображено на рис. 1.

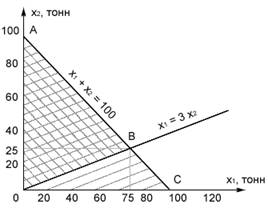
Рис.1. - Графічна інтерпретація задачі оптимізації

Внаслідок позитивних значень x1 і x2 (x1 ≥ 0; x2 ≥ 0) роз’вязання варто шукати в першому квадранті. Обмеження за сумарним випуском (x1 + x2 ≤ 100) звужує область пошуку до трикутника ОАС, який знаходиться всередині обмеженого зверху прямою x1 + x2 = 100. Обмеження x1 ≤ 3 x2 ще більш звужує область припустимих за умовою задачі значень x1 і x2, укладаючи її в трикутник ОАВ, обмежений знизу прямою x1 ≤ 3 x2. Серед усіх значень x1 і x2, ув'язнених всередині ОАВ, оптимальним відповідає тока В. У цій точці, що відповідає координатам x1 = 75; x2 = 25, досягається найбільше з припустимих значень x1, рівне 75. До найбільшого ж значення x1 і треба прагнути, тому що перший вид продукції дає у розрахунку на одну тонну більше прибутку, ніж другий (12 > 8), тобто треба вибирати найбільше з можливих, припустимих значень x1. Оптимальному роз’вязанню відповідає, таким чином, точка B, у якій цільова функція досягає свого максимального значення

12x1 + 8x2 = 12 · 75 + 8 ·25 = 1100 тис. грн.

Легко перевірити, що усередині трикутника ОАВ будь-яке інше сполучення, крім x1 = 75; x2 = 25, забезпечує менший сумарний прибуток.

2. Транспортна задача

Розглянемо спочатку загальну постановку цієї досить складної оптимізаційної задачі і побудуємо її економіко-математичну модель, яку потім проілюструємо найпростішим прикладом.

Нехай є n постачальників товару і m його споживачів. Кожен “i” постачальник здатний поставляти споживачам за визначений час кількість товару, рівному Ni, а кожен “j” споживач має потребу в кількості товару, рівному Mj. Познаніжо через xij кількість товару, що поставляється “i” постачальником “j” споживачу. Тоді загальний обсяг постачань Q, дорівнює обсягу попиту всіх споживачів, виразиться співвідношенням:

Q = , (1)

де Nj = є сума постачань усім m споживачам з боку “i” постачальника.

Mj = є сума потреб “j” споживача, засвідчуваних постачальниками всіх n постачальників.

Приймемо далі, що вартість перевезення товару “i” постачальником “j” споживачу дорівнює cij. Тоді загальна вартість перевезень, що залежать від прикріплення “i” постачальника до “j” споживача, тобто від значень xij дорівнює

F (xij) = , i=1,2…n;j=1,2…m (2)

Оптимізаційна задача полягає в тому, щоб знайти значення xij, тобто величини постачань (перевезень) товару від кожного постачальника до кожного споживача, при яких загальна вартість перевезень F(x11, x12, … xij, … xnm) буде мінімальною. Роз’вязання задачі повинне задовольняти таким обмеженням:

1) усі значення xij ненегативні, тобто

xij ≥ 0, (3)

2) можливість перевезень і запити споживача задовольняються цілком, що виражено співвідношенням (1).

Економіко-математична модель транспортної задачі, у поданому виді, яка характеризується цільовою функцією (2) і обмеженнями (1), (3), являє оптимізаційну модель задачі лінійного математичного програмування. Роз’вязання таких задач при великих значеннях кількості постачальників товару “n” і кількості споживачів товару “m” вимагає застосування складних математичних методів. Тому проілюструємо роз’вязання транспортної задачі на простому прикладі, в якому відшукання оптимального роз’вязання не складе великої праці.

Нехай є два постачальники і три споживачі товару. Можливості постачання і попит споживачів, а також вартість перевезень одиниці вантажу наведені в такій таблиці:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--