Контрольная работа: Застосування методу Монте-Карло для кратних інтегралів
Зміст
Вступ
1.Загальна схема методу Монте-Карло
1.1 Оцінка похибки методу Монте-Карло
2. Обчислення кратних інтегралів методом Монте-Карло
2.1 Принцип роботи методу Монте–Карло
3. Програма обчислення кратного інтеграла методом Монте-Карло
3.1 Програма складена на мові програмування TURBO PASCAL 7.0
3.2 Програма складена в Matematica
3.3 Результат програми
Висновок
Джерела використаної інформації
Вступ
Метод Монте-Карло можна визначити, як метод моделювання випадкових величин з метою обчислення характеристик їхнього розподілу.
Виникнення ідеї використання випадкових явищ в області наближених обчислень прийнято відносити до 1878 року, коли появилась праця Холла про визначення числа p за допомогою випадкових кидань голки на розграфлений паралельними лініями папір. Суть цієї праці полягає в тому, щоб експериментально відтворити подію, імовірність якої виражається через число p, і приблизно оцінити цю імовірність. Багато праць по методу Монте-Карло появилися в 1955-1956 роках. Тому, можна зробити висновок про широке застосування методу Монте-Карло для вирішення прикладних задач з різних областей науки та техніки
Спочатку метод Монте-Карло використовувався головним чином для вирішення задач нейтронної фізики, де традиційні числові методи виявилися мало придатними. Далі його вплив поширився на широкий класс задач статистичної фізики, дуже різних по своєму змісту.
Метод Монте-Карло зробив і продовжує робити суттєвий вплив на розвиток методів обчислення математики (наприклад, розвиток методів чисельного інтегрування) і при розв’язанні багатьох задач успішно поєднується з іншими обчислювальними методами та доповнює їх. Його використовують в першу чергу в тих задачах, в яких допускається теоретично-імовірний опис. Це пояснюється як природністю отримання результату з деякою заданою імовірністю в задачах з імовірним змістом, так і істотним спрощенням процедури розв’язання.
1. Загальна схема методу Монте-Карло
Ідея методу Монте-Карло полягає в наступному: потрібно знайти значення а деякої досліджуваної величини. Для цього вибирають таку випадкову величину Х, математичне очікування якої рівне а: М(Х)=а.
На практиці поступають таким чином: проводять n випробувань, в результаті яких дістають n можливих значень Х; потім знаходять їхнє середнє арифметичне 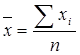 і приймають x в якості оцінки (приблизного значення) a* шуканого числа a:
і приймають x в якості оцінки (приблизного значення) a* шуканого числа a:
![]() .
.
Оскільки метод Монте-Карло вимагає проведення великого числа випробувань, його часто називають методом статистичних випробувань. Теорія цього методу вказує, як найбільш доцільно вибрати випадкову величину Х, як знайти її можливі значення. В дійсності, розробляються способи зменшення дисперсії використовуваних випадкових величин, в результаті чого зменшується похибка, допустима при заміні шуканого математичного очікування а його оцінкою а* .
Оцінка похибки методу Монте-Карло
Нехай для отримання оцінки a* математичного сподівання а випадкової величини Х було проведено n незалежних випробовувань (розіграно n можливих значень Х) і по них була знайдена вибіркова середня ![]() , яка прийнята в якості шуканої оцінки:
, яка прийнята в якості шуканої оцінки: ![]() . Звичайно, якщо повторити ще раз процедуру випробовування, то будуть отримані інші можливі значення Х, звідси і друга середня, а отже, і друга оцінка a* . Вже звідси випливає, що отримати точну оцінку математичного очікування неможливо. Звичайно, виникає запитання про розмір допустимої похибки. Обмежимось відшуканням лише верхньої границі d допустимої похибки з заданою імовірністю (вірністю) g:
. Звичайно, якщо повторити ще раз процедуру випробовування, то будуть отримані інші можливі значення Х, звідси і друга середня, а отже, і друга оцінка a* . Вже звідси випливає, що отримати точну оцінку математичного очікування неможливо. Звичайно, виникає запитання про розмір допустимої похибки. Обмежимось відшуканням лише верхньої границі d допустимої похибки з заданою імовірністю (вірністю) g:
![]() .
.
Верхня границя похибки d, яка нас цікавить, є не що інше, як «точність оцінки» математичного очікування по вибірковій середній за допомогою довірчих інтервалів. Розглянемо наступні три випадки.
Випадкова величина Х розподілена нормально і її середнє квадратичне відхилення d відоме.
В цьому випадку з імовірністю g верхня границя похибки
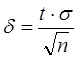 , (*)
, (*)
--> ЧИТАТЬ ПОЛНОСТЬЮ <--