Курсовая работа: Аффинные преобразования

Преобразования - движение и подобие - являются частными случаями аффинных, так как в силу свойств движения и подобия для них выполнены все требования определения аффинных преобразований.

Приведем пример аффинного преобразования, не сводящегося к ранее рассмотренным. С этой целью сначала рассмотрим параллельное проектирование плоскости на плоскость.

Пусть даны плоскости: w и w1 прямая l(направление проектирования), не параллельная ни одной из этих плоскостей (рис.2). Точка Аєw называется проекцией точки А1єw1, если АА1||l , то прямая АА1 называется проектирующей прямой. Параллельное проектирование представляет собой отображение плоскости w1 на w.

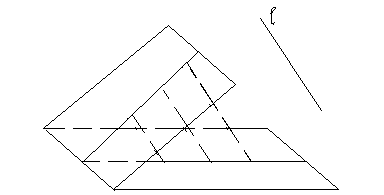
рис.2

Отметим следующие свойства параллельного проектирования.

1) Образом всякой прямой а1 является прямая.

В самом деле, прямые, проектирующие точки прямой а1, образуют плоскость (она проходит через а1 параллельно l), которая при пересечении с wдает образ прямой а1 – прямую а(рис.2).

2) Отношение, в котором точка делит отрезок, сохраняется, т.е.

(рис.2)

Сразу следует из теоремы о пересечении сторон угла параллельными прямыми.

Перейдем непосредственно к построению примера аффинного преобразования.

Возьмем два экземпляра плоскости w и один из них переместим в другое положение w1(рис.3). Новое положение какой-либо точки Аєwобозначим А1єw1. Теперь плоскость w1 спроектируем в каком-нибудь положении на w, проекцию точки А1 обозначим А'.

Получилось преобразование плоскости w на себя, при котором . В силу симметричных свойств параллельного проектирования для данного преобразования выполняются оба требования определенного аффинного преобразования, следовательно, построенное сейчас преобразование –перспективно- аффинное.

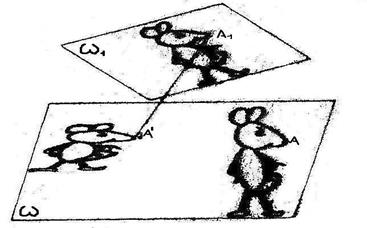
рис.3

3)Основная теорема. Каковы бы ни были 2 аффинных репера и , существует единственное аффинное преобразование, которое первый переводит во второй.

Существование. Рассмотрим преобразование а, которое произвольную точку А, имеющую в репере R координаты (х,у), переводит в точку А', имеющую в репере R' те же координаты (рис.4). Очевидно, что а(R)=R'. Покажем, что а - аффинное преобразование.

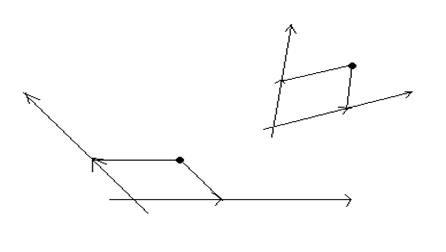
рис. 4

Образом прямой l, имеющей в репере R уравнение ах+ву+с=0, будет линия l', которая в R' имеет то же самое уравнение. Значит, l'- прямая(рис.5). Следовательно, образом произвольной прямой является прямая.

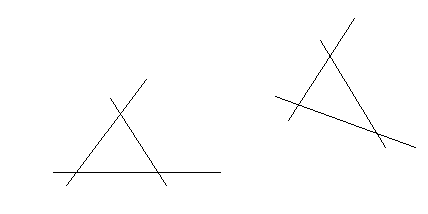
рис. 5

Пусть теперь точка С(х,у) делит отрезок, соединяющий точки А(х1,у1), В(х2,у2) в отношении

А так как образы этих точек- А',В',С' имеют те же координаты(в другой системе), то и, следовательно,

Итак для преобразования α выполнены оба требования определения, значит α- аффинное преобразование.

Единственность доказательства от противного. Пусть существует два аффинных преобразования α1 и α2, при которых . Тогда найдется такая точка А, что , где (рис.6). Обозначим через К точку пересечения прямых ОА и Е1Е2(если эти прямые параллельны, то надо взять Е1А, ОЕ2, если и эти прямые параллельны, надо взять Е2А и ОЕ1). Так как , то образом точки К будет точка К'1-точка пересечения прямых . В силу определения аффинного преобразования:

Аналогично для преобразования α2.