Курсовая работа: Аффинные преобразования

рис. 6

Первое из этих равенств показывает, что точки К'1 и К'2 совпадают, а тогда из второго следует А'1=А'2, что противоречит А. Полученное противоречие доказывает теорему.

Основную теорему можно сформулировать иначе: каковы бы ни были два треугольника, существует единственное аффинное преобразование, переводящее один в другой.

Доказанная основная теорема делает понятие аффинного преобразования конструктивным. Аффинное преобразование задается парой произвольных аффинных реперов.

4)Уравнения аффинного преобразования получаются из основной теоремы и формул преобразования аффинных координат точно так же, как и уравнения движения и подобия. Пусть даны два репера и (рис. 7).

рис. 7

O'(c1,c2),

OM'=OO'+O'M'

получаются уравнения:

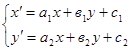
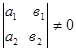
Эти уравнения записаны в аффинной системе координат. В частности они действуют и в прямоугольных декартовых координатах.

2.2 Свойства аффинного преобразования

1. Образом параллельных прямых являются параллельные прямые.

Доказательство от противного. Предположим, что образом параллельных прямых l и m являются пересекающиеся в точке А' прямые l' и m'(рис.8). В силу взаимной однозначности преобразования точка имеет прообраз, который обозначим А. Но так как А'єl', то Аєl. Аналогично Аєm. Это противоречит параллельности прямых l и m.

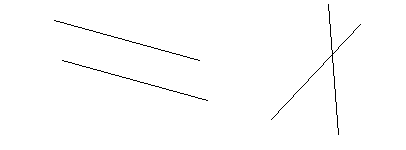
рис. 8

2.При аффинном преобразовании сохраняется отношение двух отрезков, расположенных на одной прямой: (рис.9)

В самом деле, по определению аффинного преобразования:

.

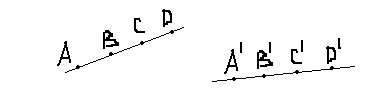
рис. 9

3.При аффинном преобразовании сохраняется отношение параллельных отрезков.

Дано: АВ||СD. По свойству 2 будет также А'В'||С'D'(рис.10)

Надо доказать: