Курсовая работа: Алгебраические группы матриц

Математический факультет

Кафедра алгебры и геометрии

Курсовая работа

АЛГЕБРАИЧЕСКИЕ ГРУППЫ МАТРИЦ

Исполнитель:

студентка группы H.01.01.01 М-42

Мариненко В.В.

Научный руководитель:

доктор физико-математических наук,

профессор Скиба С.В.

Гомель 2003

Содержание

Введение

1. Алгебраические группы матриц

1.1 Примеры алгебраических групп матриц

1.2 О полугруппах

1.3 Компоненты алгебраической группы

1.4 О -группах

2 Ранг матрицы

2.1 Возвращение к уравнениям

2.2 Ранг матрицы

2.3 Критерий совместности

3 Линейные отображения. Действия с матрицами

3.1 Матрицы и отображения

3.2 Произведение матриц

3.3 Квадратные матрицы

Заключение

Список использованных источников

Введение

Множество матриц -ой степени над будем рассматривать как аффинное пространство с имеющейся на ней полиномиальной топологией. Алгебраические группы матриц определяются как невырожденные части алгебраических множеств из , являющиеся группами относительно обычного матричного умножения. Простейший пример такой группы - общая линейная группа . В настоящем параграфе мы начнем систематическое изучение алгебраических матричных групп.

Все топологические понятия относятся к полиномиальной топологии; черта обозначает замыкание в , диез - замыкание в , бемоль - взятие невырожденной части, т. е. - совокупность всех невырожденных матриц из . Иногда, допуская вольность, мы употребляем для групп те же понятия, что и для подлежащих алгебраических множеств, - например, говорим об общих точках групп; это не должно вызывать недоразумений.

1. Алгебраические группы матриц

1.1 Примеры алгебраических групп матриц

Классические матричные группы - общая, специальная, симплектическая и ортогональная :

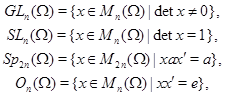
где

--> ЧИТАТЬ ПОЛНОСТЬЮ <--