Курсовая работа: Алгебраические группы матриц
Диагональная группа ![]() , группы клеточно-диагональных матриц данного вида. Треугольная группа
, группы клеточно-диагональных матриц данного вида. Треугольная группа ![]() (для определенности --- с нижним нулевым углом), унитреугольная группа
(для определенности --- с нижним нулевым углом), унитреугольная группа ![]() (треугольные матрицы с единичной диагональю), группы клеточно-треугольных матриц данного вида.
(треугольные матрицы с единичной диагональю), группы клеточно-треугольных матриц данного вида.
Централизатор произвольного множества из ![]() в алгебраической группе
в алгебраической группе ![]() , нормализатор замкнутого множества из
, нормализатор замкнутого множества из ![]() в
в ![]() .
.
Пересечение всех алгебраических групп, содержащих данное множество матриц ![]() из
из ![]() --- алгебраическая группа. Она обозначается
--- алгебраическая группа. Она обозначается ![]() и называется алгебраической группой, порожденной множеством
и называется алгебраической группой, порожденной множеством ![]() .
.
Каждую алгебраическую линейную группу из ![]() можно изоморфно --- в смысле умножения и полиномиальной топологии --- отождествить с замкнутой подгруппой из
можно изоморфно --- в смысле умножения и полиномиальной топологии --- отождествить с замкнутой подгруппой из ![]() в силу формулы
в силу формулы
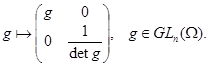
Такое отождествление позволяет при желании ограничиться рассмотрением только таких групп матриц, которые сами являются алгебраическими множествами (а не их невырожденными частями). Это дает другое оправдание тем вольностям в терминологии, которые упоминались в начале параграфа.
Множество всех матриц из ![]() , оставляющих инвариантной заданную невырожденную билинейную форму
, оставляющих инвариантной заданную невырожденную билинейную форму ![]() на
на ![]() .
.
Пусть ![]() --- алгебра над
--- алгебра над ![]() конечной размерности
конечной размерности ![]() (безразлично, ассоциативная или нет),
(безразлично, ассоциативная или нет), ![]() --- группа всех ее автоморфизмов. Фиксируя в
--- группа всех ее автоморфизмов. Фиксируя в ![]() какую-нибудь базу
какую-нибудь базу ![]() и сопоставляя автоморфизмам алгебры
и сопоставляя автоморфизмам алгебры ![]() их матрицы в этой базе, мы получим на
их матрицы в этой базе, мы получим на ![]() строение алгебраической группы. Действительно, пусть
строение алгебраической группы. Действительно, пусть
![]()
т. е. ![]() --- структурные константы алгебры
--- структурные константы алгебры ![]() . Пусть далее
. Пусть далее
![]()
где ![]() . Тогда
. Тогда ![]() задается в матричных координатах
задается в матричных координатах ![]() очевидными полиномиальными уравнениями, вытекающими из соотношений
очевидными полиномиальными уравнениями, вытекающими из соотношений
![]()
Указать в приведенных выше примерах определяющие уравнения, найти общую точку, если она есть.
В дальнейшем нам встретится еще много примеров и конструкций алгебраических матричных групп.
1.1.1 Если матричная группа ![]() содержит алгебраическую подгруппу
содержит алгебраическую подгруппу ![]() конечного индекса, то
конечного индекса, то ![]() сама алгебраическая.
сама алгебраическая.
Доказательство. Пусть ![]() - аннулятор группы
- аннулятор группы ![]() в
в ![]() ,
, ![]() - его корень в
- его корень в ![]() . Надо показать, что
. Надо показать, что ![]() . Пусть, напротив,
. Пусть, напротив, ![]() . Пусть
. Пусть ![]() - смежные классы
- смежные классы ![]() по
по ![]() . Для каждого
. Для каждого ![]() выберем многочлен
выберем многочлен

и положим
![]()
Очевидно, ![]() ,
, ![]() . Получили противоречие.
. Получили противоречие.
Пусть ![]() --- алгебраическая группа,
--- алгебраическая группа, ![]() ,
, ![]() --- подмножество и замкнутое подмножество из
--- подмножество и замкнутое подмножество из ![]() . Тогда множества
. Тогда множества

где ![]() , замкнуты. Если
, замкнуты. Если ![]() тоже замкнуто и
тоже замкнуто и ![]() --- общее поле квазиопределения для
--- общее поле квазиопределения для ![]() ,
, ![]() ,
, ![]() , то
, то ![]() ,
, ![]() ,
, ![]() квазиопределены над
квазиопределены над ![]() . В частности, если существует хотя бы одно
. В частности, если существует хотя бы одно ![]() с условием
с условием ![]() (соответственно,
(соответственно, ![]() ,
, ![]() ), то можно считать, что
), то можно считать, что ![]() (см. 7.1.5).
(см. 7.1.5).
Если на множестве ![]() выполняется теоретико-групповое тождество
выполняется теоретико-групповое тождество ![]() , то оно выполняется и на его замыкании
, то оно выполняется и на его замыкании ![]() . В частности, коммутативность, разрешимость, нильпотентность матричной группы сохраняются на ее замыкании в полиномиальной топологии.
. В частности, коммутативность, разрешимость, нильпотентность матричной группы сохраняются на ее замыкании в полиномиальной топологии.
1.2 О полугруппах
Определим действие элементов из ![]() на рациональные функции из
на рациональные функции из ![]() ,
, ![]() , полагая
, полагая
![]()
Для каждого ![]() отображение
отображение ![]() (сдвиг аргумента) есть автоморфизм поля
(сдвиг аргумента) есть автоморфизм поля ![]() . Отображение
. Отображение ![]() есть изоморфизм полной линейной группы
есть изоморфизм полной линейной группы ![]() в группу автоморфизмов расширения
в группу автоморфизмов расширения ![]() .
.