Курсовая работа: Алгоритмы преобразования ключей

TBTreeNode = record {узелдерева}

Count: Integer;

PreviousNode: PBTreeNode;

Items: array[0..NumberOfItems+1] of record

Value: ItemType;

NextNode: PBTreeNode;

end;

end;

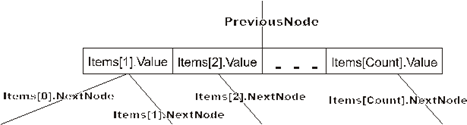
У элемента Items[0] будет использоваться только поле NextNode. Дополнительный элемент Items[NumberOfItems+1] предназначен для обработки переполнения, о чем будет рассказано ниже, где будет обсуждаться алгоритм добавления элемента в B-дерево.

Поскольку дерево упорядочено, то Items[1].Value<Items[2].Value<…< Items[Count].Value. Указатель Items[i].NextNode указывает на поддерево элементов, больших Items[i].Value и меньших Items[i+1].Value. Понятно, что указатель Items[0].NextNode будет указывать на поддерево элементов, меньших Items[1].Value, а указатель Items[Count].NextNode – на поддерево элементов, больших Items[Count].Value.

Само дерево можно задать просто указанием корневой вершины. Естественно, что у такой вершины PreviousNode будет равен nil.

Type

TBTree = TBTreeNode;

Прежде чем рассматривать алгоритмы, соберем воедино все требования к B-дереву :

1. каждый узел имеет не более NumberOfItems сыновей;

2. каждый узел, кроме корня, имеет не менее NumberOfItems/2 сыновей;

3. корень, если он не лист, имеет не менее 2-х сыновей;

4. все листья расположены на одном уровне (дерево сбалансировано);

5. нелистовой узел с k сыновьями содержит не менее k-1 ключ.

Из всего вышесказанного можно сразу сформулировать алгоритм поиска элемента в B-дереве.

Поиск элемента в B-дереве

Поиск будем начинать с корневого узла. Если искомый элемент присутствует в загруженной странице поиска, то завершаем поиск с положительным ответом, иначе загружаем следующую страницу поиска, и так до тех пор, когда либо найдем искомый элемент, либо не окажется «следующей страницы поиска» (пришли в лист B-дерева).

Посмотрим на примере, как это будет работать. Пусть мы имеем такое дерево (в наших примерах мы будем разбирать небольшие деревья, хотя в реальности B-деревья применяются при работе с большими массивами информации):

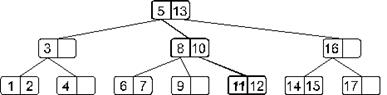
Будем искать элемент 11. Сначала загрузим корневой узел. Эта страница поиска содержит элементы 5 и 13. Наш искомый элемент больше 5, но меньше 13. Значит, идем по ссылке, идущей от элемента 5. Загружаем следующую страницу поиска (с элементами 8 и 10). Эта страница тоже не содержит искомого элемента. Замечаем, что 11 больше 10 – следовательно, двигаемся по ссылке, идущей от элемента 10. Загружаем соответствующую страницу поиска (с элементами 11 и 12), в которой и находим искомый элемент. Итак, в этом примере, чтобы найти элемент, нам понадобилось три раза обратиться к внешней памяти для чтения очередной страницы.

Если бы в нашем примере мы искали, допустим, элемент 18, то, просмотрев 3 страницы поиска (последней была бы страница с элементом 17), мы бы обнаружили, что от элемента 17 нет ссылки на поддерево с элементами большими 17, и пришли бы к выводу, что элемента 18 в дереве нет.

Теперь точно сформулируем алгоритм поиска элемента Item в B-дереве, предположив, что дерево хранится в переменной BTree, а функция LookFor возвращает номер первого большего или равного элемента узла (фактически производит поиск в узле).

function BTree.Exist(Item: ItemType): Boolean;